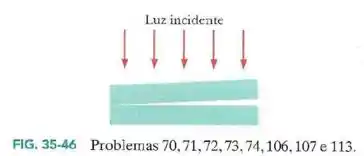
Duas placas retangulares de vidro () estão em contato em uma das extremidades e separadas na outra extremidade (Fig.35-46). Um feixe de luz com um comprimento de onda de incide perpendicularmente à placa superior. O ar entre as placas se comporta como um filme fino.
Um observador que olha para baixo através da placa superior vê nove franjas escuras e oito franjas claras.
Quantas franjas escuras são vistas se a distância máxima entre as placas aumenta ?
Passo 1
Como o observador vê uma franja escura a mais que as franjas claras, então deve ser o caso que temos uma franja escura em cada borda do filme fino.
Isso significa que para a distância máxima entre as placas, vale a condição de interferência destrutiva, que no caso (ar envolta de placas de vidro) é:
Como o filme é ar, temos
Passo 2
Lembrando que temos franjas escuras, essa franja é a de ordem , pois a contagem começa com . O comprimento de onda da luz é
A espessura nesse ponto é:
Passo 3
Se aumentarmos a distância máxima das placas em , ela vai passar a ser:
Se substituirmos isso na condição de interferência, acharemos um mínimo de nova ordem:
Ou seja, o novo mínimo é de ordem , o que nos diz que agora temos mínimos de interferência.
Resposta
Veremos franjas escuras para a nova distância.