A componente vertical da velocidade de aterrissagem de um paraquedas deve ser inferior a . A massa total do paraquedas com o paraquedista é . Determine o mínimo diâmetro do paraquedas aberto.
Passo 1
Fala, galera! Vamos agora fazer um projeto e paraquedas, pra não cair de cara na prova. Ahah
Bom, antes de começarmos a calcular qualquer coisa do problema, precisamos entender bem a situação. O enunciado traz um sistema composto por paraquedista e seu paraquedas (cuja massa é conhecida e igual a ).
Sabemos que na queda, além da força peso (), também verificamos a força de arrasto () causada pelo ar, como observamos abaixo:
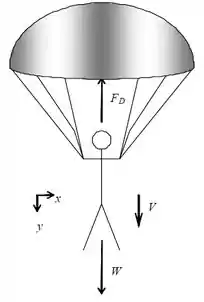
Nessa situação, consideramos o paraquedas como um hemisfério (com extremidade aberta – côncava – para o escoamento), cujo diâmetro precisamos determinar.
Como a velocidade da queda é constante (), podemos considerar que o movimento é uniforme e, portanto, a soma das forças deve ser igual a zero.
Passo 2
Vamos, então, calcular as forças envolvidas! O peso () será igual a:
Já a força de arrasto () é dada pela expressão:
Para esse tipo de geometria, vemos na tabela que o coeficiente de arrasto () é dado por:
Já sabemos a densidade do ar () e a velocidade (), logo a área é nossa única incógnita. Como as forças se anulam, podemos escrever que:
Isolando a área:
E substituindo essa galera:
OBS: Note que avaliar o sistema paraquedista-paraquedas em movimento descendente (pra baixo) no ar “parado” é equivalente a avaliar o sistema paraquedista-paraquedas parado e o ar em movimento ascendente (pra cima). Isso está atrelado ao conceito físico de velocidade relativa.
Passo 3
A escolha da área nesse momento é um ponto crucial. Qual área vamos utilizar?
Você poderia pensar o seguinte: “Bom, a área de um hemisfério é metade da área e uma esfera, então eu jogo essa expressão!”. Pois é, mas daria errado! Mas por quê?
A área que interessa é somente a área perpendicular ao escoamento. Esse pensamento é análogo ao que fazemos para calcular a pressão sobre uma área não-uniforme, nós só pegamos a componente normal à força.
Se considerássemos a componente paralela, estaríamos avaliando o movimento lateral do paraquedas, ou seja, se ele estaria indo para a esquerda ou direita. Como estamos interessados no movimento vertical (queda), só é importante pra gente a área da projeção ilustrada na imagem abaixo:
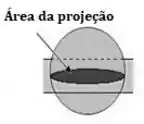
Temos que o diâmetro do círculo na projeção é o mesmo diâmetro do paraquedas. Portanto, podemos escrever:
OBS: Sempre aproximaremos o diâmetro “para cima”, pois sabemos que mantidas as demais condições, quanto maior o diâmetro, maior será a área do paraquedas e, consequentemente, maior será a força de arrasto. Se fosse menor que esse diâmetro, observaríamos que: .