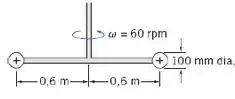
Você é um engenheiro recém-formado e decide fazer com que um misturador rotativo seja melhorado por meio da substituição dos discos por anéis. Os anéis podem ter a vantagem adicional de fazer com que o misturador misture mais eficientemente. Se o misturador absorve 350 W a 60 rpm, refaça o projeto. Existe uma restrição no projeto de que o diâmetro externo dos anéis não deve exceder 125 mm.
Passo 1
Agora a estratégia é outra, padawan! Temos uma potência fixada e queremos projetar um misturador rotativo com anéis (e não mais discos, como no anterior).
Sabemos que a potência () é função do torque e pode ser descrita como:
Como o torque () é dado pelo produto entre a força aplicada e a distância ao eixo, temos que a força de arrasto será dada por:
Passo 2
Lembra da equação que descreve a força de arrasto? Podemos expressá-la como:
Observe que os termos , e independem do raio interno do anel, então já podemos determiná-los.
O coeficiente de arrasto () é função do tipo de geometria do sistema. Pela tabela, temos que o para objetos anulares é dado por:
Além disso, a velocidade linear ( é dada por:
Dessa forma, a única variável a ser determinada é a área do anel ():
Passo 3
Como a área é função dos diâmetros interno e externo do anel e nos foi informado que o anel tem diâmetro externo máximo de , podemos escrever a área como função somente do diâmetro interno:
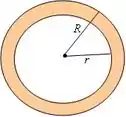
Assim: