A resistência ao movimento de uma boa bicicleta sobre um pavimento liso é decorrente, quase que inteiramente, do arrasto aerodinâmico. Considere que a massa total de ciclista e bicicleta é . A área frontal, medida de uma fotografia, é . Experiências em uma colina com declive de 9% mostram que a velocidade terminal é A partir desses dados, o coeficiente de arrasto é estimado como . Verifique os cálculos do coeficiente de arrasto. Estime a distância necessária para que o ciclista e bicicleta desacelerem de para , enquanto o ciclista descansa nos pedais após atingir o piso plano.
Passo 1
Aqui a geometria do sistema não se enquadra em nenhum tipo tabelado, pode conferir que não tem “bicicleta” naqueles tipos de geometria da tabela ahah
Bom, então, como saber o coeficiente de arrasto? Nesse problema o enunciado nos fornece somente uma estimativa para seu valor () e nos pede para verificar. Então, o coeficiente será exatamente nossa incógnita e, portanto, precisamos encontrar a equação que rege o fenômeno e determinar os demais parâmetros.
O sistema avaliado consiste no conjunto ciclista-bicicleta como encontramos na imagem abaixo:
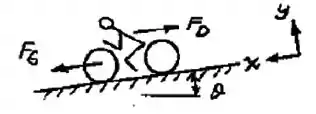
Lembra das aulas de física de plano inclinado? Pois é, vamos utilizar decompor aqui as forças que atuam no nosso “bloquinho”:
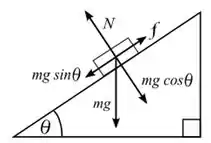
Já sabemos os valores de: e . Agora, precisamos encontrar o valor de , a fim de determinarmos a componente peso na direção .
Foi informado que a declividade do plano é de , portanto, podemos relacioná-la com a tangente do ângulo da seguinte forma:
Dessa maneira, já temos todos os parâmetros para o cálculo de :
Esse foi o valor calculado, vamos comparar com a estimativa inicial. O erro relativo da estimativa em relação ao cálculo é de:
Erros superiores a 10% geralmente não são aceitos, mas numa visão menos conservadora, poderíamos assumir o valor como satisfatório.
Passo 2
Agora é a parte do enunciado! Vamos calcular a distância necessária para que o ciclista sofra uma desaceleração de para . A força resultante sobre um corpo é dada por:
Como o enunciado afirma que a resistência ao movimento é quase que interiamente devido à força de arrasto, temos que:
Como estamos interessados na distância para que haja a desaceleração (e não no tempo), podemos reescrever a velocidade como sendo:
Com a notação de Leibniz, podemos substituir o infinitesimal na equação da força resultante:
Integrando a equação, teremos:
Utilizando o coeficiente de arrasto () estimado:
Resposta
CONFERIR RESOLUÇÃO! VERIFICAR SE A FORÇA RESULTANTE NÃO DEVERIA SER A COMPONENTE DO PESO EM X MENOS A FORÇA DE ARRASTO!