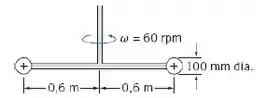
Um misturador rotativo é construído com dois discos circulares, conforme mostrado. O misturador é acionado a dentro de um grande vaso contendo uma solução de salmoura (). Despreze o arrasto sobre as hastes e o movimento induzido no líquido. Estime o torque e a potência mínimos requeridos para acionar o misturador.
OBS: A sigla significa “specific gravity” e se refere a densidade relativa da substância, ou seja, a razão entre a densidade da substância sobre a densidade da água.
Passo 1
Vamos pensar um pouco na nossa estratégia de cálculo?
O enunciado nos pede para calcular o torque e a potência requerida para que o misturador possa operar. Ambos são funções da força a qual o fluido é submetido, então precisamos calcular essa força.
Diz aí: qual o nome dessa força? Isso mesmo! A força de arrasto! Como já vimos, a força de arrasto () pode ser expressa por:
Vamos, então, encontrar os parâmetros a serem determinados começando pela área do disco (:
A velocidade linear ( é dada por:
Nós já vimos que existem valores tabelados para o coeficiente de arrasto () de geometrias específicas, inclusive para um disco, desde que .
Então, bora verificar o número de Reynolds desse escoamento. Vamos utilizar como comprimento característico o diâmetro do disco e já sabemos a densidade da salmoura:
Ótimo! Podemos usar o valor da tabela!
Pela tabela, o coeficiente de arrasto para um disco é dado por:
Dessa maneira, é possível calcularmos a força de arrasto ():
OBS: A densidade é , pois a definição de densidade relativa () é dada por:
Passo 2
Sabemos que o torque () é dado pelo produto entre a força aplicada e a distância do eixo de rotação, logo:
Assim, conseguimos calcular a potência mínima requerida () para acionar o misturador: