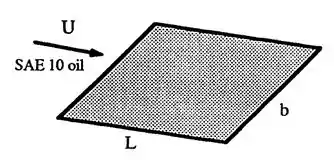
Uma placa plana fina de 55 cm por 110 cm está imersa em um fluxo de 6 m/s de óleo SAE 10 a 20°C. Calcule o arrasto total de atrito, caso o fluxo seja paralelo (a) ao lado maior ou (b) ao lado menor.

Dados: ,

Coeficiente de arrasto (placa plana, sem gradiente de pressão, laminar)

Coeficiente de arrasto (placa plana, sem gradiente de pressão, turbulento)

Escoamento Laminar:

Escoamento Turbulento:

Opa! Temos nesse exercício uma geometria diferente: uma placa plana fina. Além disso, vamos considerar que o arrasto de pressão é quase nulo. Assim, o arrasto total de atrito será o arrasto total, que vimos na teoria :D

Ué? Mas podemos considerar isso? Sim! Inclusive, os valores de coeficiente de arrasto dados são válido para arrasto viscoso sem gradiente de pressão.

Queremos saber então a força de arrasto

Conhecemos a massa específica e a velocidade. A área é duas vezes a área da placa, pois o escoamento está passando nos 2 lados dessa placa fina. Ficamos assim:

Para encontrar o coeficiente de arrasto, vamos utilizar uma das expressões fornecidas no enunciado. Uma serve para escoamento laminar e outra para turbulento. Vamos então calcular Reynolds para o escoamento sobre a placa:

L é o comprimento paralelo ao escoamento. Na letra a, o exercício pediu para considerar que o fluxo fosse paralelo ao lado maior. Nesse caso, L = 110 cm = 1,1 m. Substituindo

O enunciado deu a referência de escoamento laminar como . Logo, esse é um escoamento laminar. Por isso, vamos usar essa fórmula do coeficiente de arrasto

Assim, vamos calcular a força de arrasto

Essa é a força de arrasto considerando o fluxo de fluido paralelo ao lado maior.