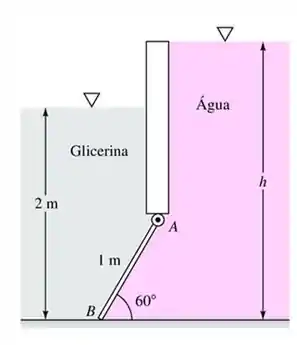
A comporta na Figura abaixo é uma massa homogênea de , de largura, é articulada em e está apoiada sobre um fundo liso em . Todos os fluidos estão a . Para qual profundidade da água a força no ponto será zero?
Passo 1
Essa é a questão que mistura tudo que aprendemos, pois temos a comporta exposta a dois fluidos. A comporta está inclinada.
Sabemos que para calcular a força de pressão precisamos saber a posição do centro de gravidade. Então iremos achar a posição do centro de gravidade.
Como a comporta é um retângulo, o centro de gravidade está no meio dela, assim temos:
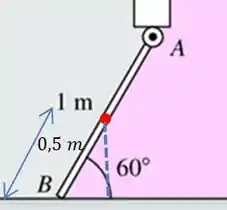
Vamos usar a relação do seno:
Agora a gente consegue calcular a profundidade do centro de gravidade.
Começando pelo lado esquerdo, o lado da glicerina:
A profundidade do centro de gravidade é:
Já no lado da água, teremos uma função, já que não sabemos o valor da coluna de água, na verdade é isso que queremos descobrir, assim:
Passo 2
Sabendo a profundidade do centro de gravidade para cada lado. E também, sabendo que a densidade da água é e da glicerina é . Conseguimos calcular a força de pressão aplicada na placa devido a cada fluido.
Já a força devido a coluna de água será uma função, tendo como variável.
Passo 3
Já encontramos as forças, agora só falta encontrar o ponto de aplicação de cada uma delas.
Começando pela força devido a glicerina, temos:
O momento de inércia da comporta retangular é:
Como o enunciado informou que a largura b é 1,2 m e pela figura temos que o comprimento L da comporta é de 1 m:
Observe que a parte que importa qual fluido se trata se cancela, sendo assim a única coisa que vai mudar de uma equação para a outra será a profundidade do centro de gravidade.
Mas vamos terminar de calcular essa posição antes de tudo:
Agora, vamos calcular a posição para a força devido a água. Usando o que já encontramos:
Passo 4
Show, temos as forças e pontos de aplicação calculados.
Sempre lembrando que esses ponto de aplicação foram calculados em relação ao centro de gravidade, no plano da placa. Não se esqueçam disso, por favor!
Então o que a gente tem é isso:
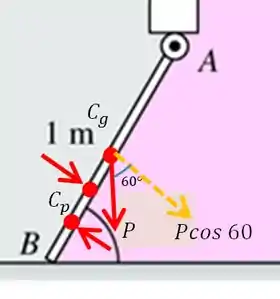
Para podermos aplicar a equação de momento, devemos decompor o peso, pois no momento irá interessar apenas a componente normal a comporta, sendo esta:
Bem, agora podemos aplicar a equação de momento, fazendo o momento em relação ao ponto .
Preste atenção que é no ponto , sendo assim a distância do centro de gravidade a este ponto é .
A distância do centro de pressão da glicerina será a posição do centro de gravidade em relação ao ponto menos a sua posição em relação ao centro de gravidade:
E o mesmo acontecerá com o centro de pressão da água:
Agora sim, aplicando a equação de momento: