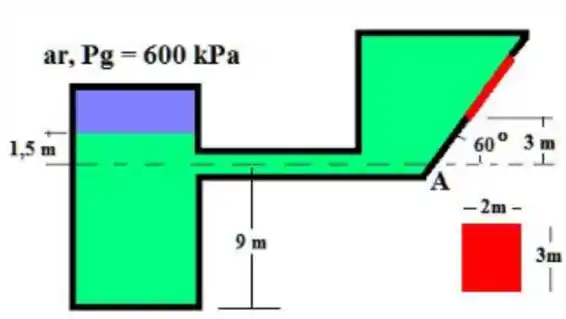
Determine a força e seu ponto de aplicação para a comporta da figura. A substância de trabalho é a água. (Este exercício exige um bom conhecimento da teoria).
Passo 1
Queremos saber a força aplicada na comporta e o ponto de aplicação, certo?
A pressão a gente viu que é:
Mas ae que vem o diferente dessa questão, a gente não tem ideia dá altura do tanque em que a comporta está localizada.
E para descobrir essa altura vamos usar o que vimos na teoria de vasos comunicantes. Lembra que dois pontos no mesmo fluido tem a mesma pressão?
Então, vamos usar isso para descobrir a altura no tanque a direita analisando esses dois pontos:
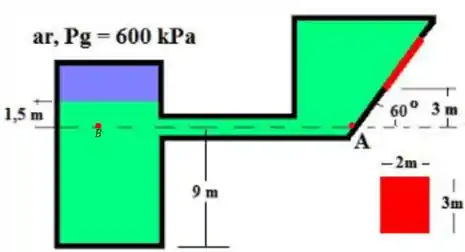
A pressão do lado esquerdo, ponto , é dada pela pressão e pela pressão da coluna de liquido , assim
Já a pressão no ponto é dada apenas pela coluna de liquido, sendo assim
Como , então vamos igualar as pressões e descobrir a profundidade do tanque a direita.
Então, temos a seguinte configuração:
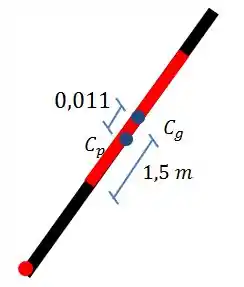
Agora falta apenas descobrirmos a posição do centro de gravidade. Vamos dar um zoom na parte da comporta e olhar só para ela. Vamos ter a seguinte configuração:
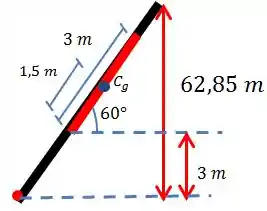
Com isso, usando a relação de
Assim, descobrimos que
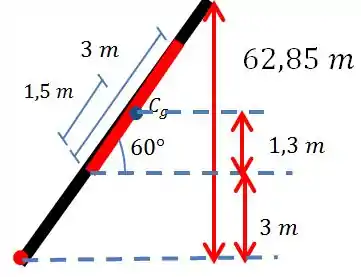
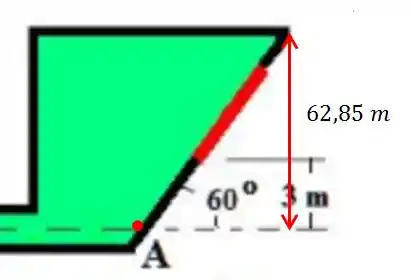
Agora a gente consegue descobrir a profundidade do centro de gravidade
Pelo desenho vemos que será:
Sendo assim, agora conseguimos calcular a força causada pela coluna de liquido.
Agora temos a profundidade e a área do portão é dada na figura no enunciado, temos:
Passo 2
Agora, vamos encontrar o ponto de aplicação, o centro de pressão.
A formula para isso é:
O ângulo que a placa faz com a horizontal é , além disso podemos cortar a densidade mássica, ficando com:
O momento de inércia de uma chapa retangular é:
Substituindo os valores que temos, chegamos em:
Lembrando que esse valor é relação ao centro de gravidade, então temos isso: