Na figura abaixo, determinar a altura e a mínima força para que a comporta permaneça em equilíbrio. A largura é unitária. Adotar e
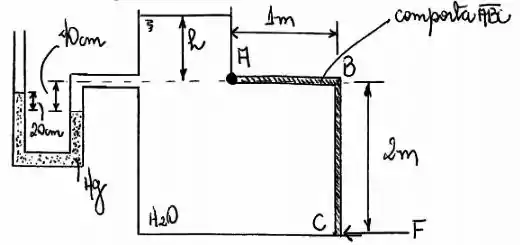
Passo 1
Vamos começar descobrindo o valor de . Para isso vamos usar o princípio de Stevin, ou seja, pegar dois pontos no mesmo fluido na mesma altura e igualar as pressões.
Porém nesse caso dois pontos não será o suficiente para gente resolver o problema, iremos precisar de 4 pontos, os seguintes 4 pontos:
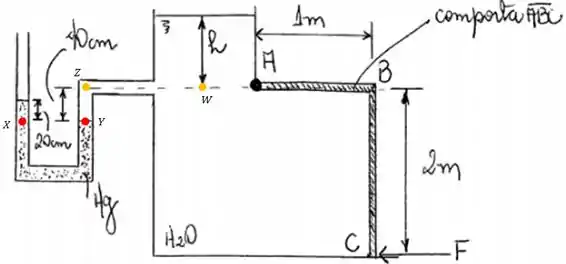
Temos que e
Beleza, vamos então primeiro montar a igualdade de pressão dos pontos laranjas.
A pressão em é devido a pressão atmosférica e a pressão de coluna de água , sendo assim vale:
Agora vamos montar a equação de pressão dos pontos em vermelho.
A pressão em é:
Já a pressão em é:
Igualando as pressões temos:
A pressão atmosférica vai se cancelar, assim sobrando apenas como variável.
Agora que sabemos a altura conseguimos saber a pressão nos pontos e .
Porque a pressão nesse ponto é importante? Pois ela ira exercer uma força na comporta, nessa região.
Como temos a ação da pressão atmosférica na região externa, vamos subtraí-la da conta, assim podemos falar que a pressão em e é:
Como temos a ação de uma pressão constante na superfície da comporta o ponto de aplicação será no centroide da superfície , sendo assim . E podemos calcular a força resultante dessa pressão usando:
A largura, foi dita unitária, 1.
Sendo assim a força aplicada na região é
Passo 2
Agora vamos descobrir a força causada na superfície da comporta. Aqui é onde acontece o que temos estudado e feito vários exercícios.
Assim, a força será dada por:
O centro de gravidade dessa superfície está localizado a do ponto , certo? Metade da chapa.
Sendo assim a profundidade do centro de gravidade é:
Tendo a profundidade do centro de gravidade conseguimos calcular a força.
Agora, só falta encontrarmos a posição em que atua essa força, ou seja, o centro de pressão:
O ângulo que a chapa faz com a superfície é , o momento de inércia de uma chapa é:
Substituindo isso temos:
Como essa posição é em relação ao centro de gravidade, então em relação ao ponto a distância seria:
E a força aplicada no ponto está a do ponto . Bem, para que precisamos saber disso? Para quando aplicarmos a equação de momento sabermos todas as distâncias.
Passo 3
Então agora vamos aplicar a equação de momento, se queremos que a peça esteja parada então,