A comporta na Figura abaixo tem de largura, está articulada em e limitada por um limitador em . A água está a . Calcule a força no limitador e as reações em A se a profundidade da água é
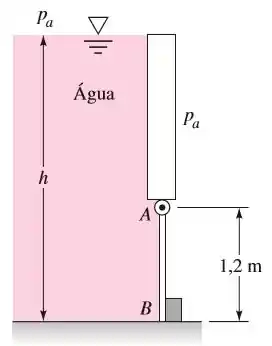
Passo 1
Para resolvermos esse item precisamos descobrir o valor da força causada pela pressão de água na comporta, no ponto onde essa pressão está sendo aplicada, . E após isso, vamos usar o fato dela estar parada para descobrir a força aplicada no limitador . Para isso vamos usar:
Como disse teremos a atuação da força de pressão no centro de pressão () e da força no limitador impedindo que a comporta abra.
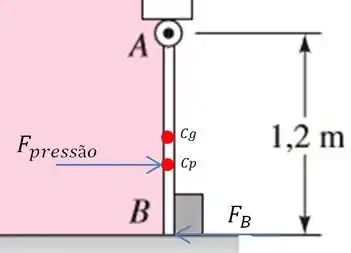
Montando a equação de momento em relação ao ponto , temos:
Lembrando que as distâncias são em relação ao ponto . E por isso fizemos a gente já tem .
E por isso para resolvermos o problema basta descobrirmos a força de pressão e a posição do centro de pressão.
Passo 2
Já sabemos como resolver, agora só falta atacar mesmo né?!
Na teoria vimos que a força de pressão é dada por:
A densidade da água a a gente sabe que é . A aceleração da gravidade é . E a profundidade do centro de gravidade a gente tem que calcular.
O centro de gravidade de uma chapa retangular fica bem no meio, assim a posição do centro de gravidade em relação ao fundo, ponto , é:
Mas a gente quer a profundidade e por isso temos que fazer a profundidade total do fluido menos a posição do centro de gravidade em relação ao fundo.
E por fim vamos calcular a área da comporta.
Podemos então calcular a força de pressão na comporta.
Passo 3
Agora vamos encontrar a posição do centro de pressão. Bem, estamos interessados só na posição , pois é dela que precisamos para aplicar a equação de momento.
Assim, na teoria vimos que a fórmula para encontrar o centro de pressão em relação ao centro de gravidade é:
O ângulo que a placa faz com a horizontal é e é
A força de pressão a gente já calculou. Por fim falta apenas o momento de inércia da placa. Como é uma placa retangular o momento de inércia é:
A base é a largura, que vale . A altura também foi dada e vale . Assim o momento de inércia é:
Jogando isso tudo na fórmula temos:
Lembrando que isso é em relação ao centro de gravidade, o que significa que a posição do centro de pressão é:
Então ficamos assim:
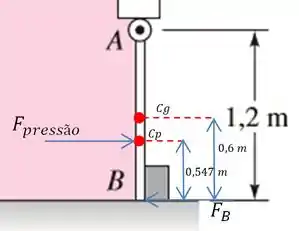
Beleza, agora podemos voltar para a equação do momento, lembrando que as distâncias devem ser em relação ao ponto .
Isolando , temos:
Passo 4
Agora queremos a reação em A.
O jeito mais fácil de fazer isso é usando o fato que para estar parado o somatório de força tem que ser zero.
As forças atuantes são: A força de reação , a força de pressão e a força de reação . Assim, temos que:
Isolando , temos:
Já encontramos o valor das duas forças, então basta substituir
Vale ressaltar que não temos a atuação de forças na direção do eixo , que é na direção da largura da comporta, por isso a reação nessa direção é zero. .