Um portão plano, de espessura uniforme, suporta água a uma certa profundidade, como abaixo. Encontre o peso mínimo que o portão deve ter para que permaneça fechado.
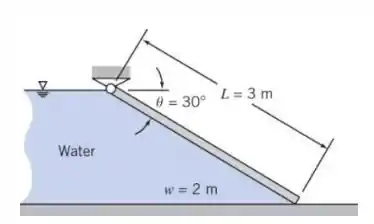
Passo 1
Agora, temos uma comporta inclinada. Sendo assim, o peso da comporta deve ser levado em conta.
O peso atua no centro de gravidade. Vamos posicionar a força peso. E decompô-la. Assim,
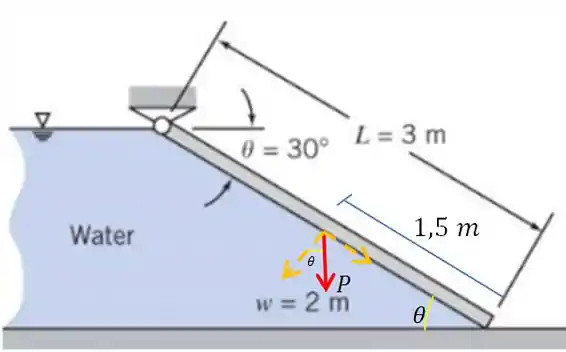
A componente que do peso que vai importar para gente é a componente perpendicular ao portão. Então lembrando daquela regrinha de decomposição. “Co-lado/Se-parado” Como queremos a componente colada com o ângulo, vamos usar o cosseno.
Assim,
Agora, falta apenas encontrarmos a força causada pela coluna de água.
Para isso vamos usar as fórmulas que aprendemos:
A densidade mássica da água a gente já viu que vale:
A profundidade do centro de gravidade a gente tem que calcular.
Bem, o que a gente tem é mais ou menos isso:
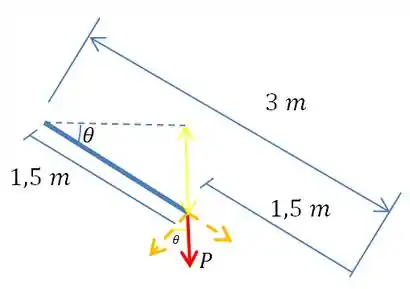
Beleza, para descobrir a profundidade do centro de gravidade, a gente vai usar a seguinte relação:
Assim,
A área do portão é só multiplicar o comprimento pela largura:
Assim, a força de pressão é:
E o centro de pressão é:
Temos quase tudo, só falta calcular o momento de inércia.
Como a placa é retangular o momento de inércia é dado por:
Agora, podemos calcular a posição do centro de pressão:
Agora, temos todas as posições e forças. Ficamos com um esquema assim:
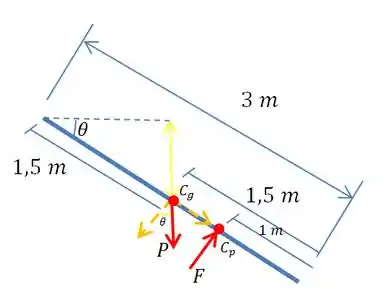
Então podemos aplicar a equação de momento. Faremos o momento em relação ao ponto de rotação do portão, isto é o pino dele. Lá em cima.
Se o peso for menor que isso o momento não será zero o que significará que o portão entrará em movimento.