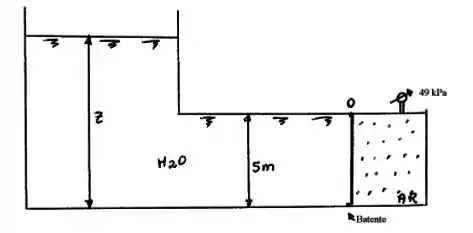
Determinar o mínimo valor de , para o qual a comporta da figura girará em torno do ponto O, se a comporta é retangular de de largura. Dado .
Passo 1
Essa questão é parecida com as que já fizemos, mas ela tem um detalhe muito importante.
Lembra na teoria quando falamos que estávamos desconsiderando a pressão atmosférica, pois ela estaria na maioria das vezes aplicada aos dois lados?
Pois bem, nesse caso a gente continua tendo a aplicação da pressão atmosférica dos dois lados.
Porém do lado externo da comporta existe uma pressão extra a da atmosférica, que o manômetro está medindo que vale .
Então vamos continuar ignorando a pressão atmosférica, mas temos que agora levar em conta a pressão do lado externo.
OBS: Observe que no lado externo temos a aplicação da pressão atmosférica mais a pressão do ar que vale . Por isso podemos não considerar a pressão atmosférica, pois ela atua tanto no lado externo quanto interno.
Bem, vamos começar a resolver o problema. Como temos pressão dos dois lados, teremos força atuando dos dois lados.
Existem duas maneiras da comporta se mexer uma é se e a outra se
Vamos primeiro começar pelo somatório de força.
Como vimos com a pressão atmosférica que a pressão de um lado anula a do outro. Podemos observar que a comporta vai começar a se mexer quando a pressão da coluna de liquido no centroide superar a pressão de ar no lado externo.
Assim, quando:
Já que para os dois lados a área da chapa é a mesma.
Então basta resolvermos a inequação:
Para descobrirmos o valor de .
Bem, dado que é uma comporta retangular o centro de gravidade é na metade do comprimento, assim valendo .
Como queremos a profundidade do centro de gravidade, basta fazer:
Tendo e sabendo a densidade mássica da água, podemos substituir os valores na inequação:
Então, chegamos que em:
Passo 2
Agora, vamos começar a analisar a segunda opção
Para essa opção vamos ter que encontrar o ponto de aplicação das duas forças.
Vamos começar com a força externa, como a pressão no lado externo é constante então o ponto de aplicação é no centro de gravidade.
Sendo assim o ponto estaria a do ponto .
E a força aplicada nesse ponto seria:
Agora vamos analisar a região interna, a força vai ser dada em função de .
E o ponto de aplicação será o centro de pressão que é calculado por:
Podemos simplificar já que o ângulo que a comporta faz com a horizontal é .
A área já sabemos que é a profundidade do centro de gravidade também já conhecemos,
Só falta o momento de inércia, esse a gente tem que calcular:
Substituindo, temos:
Esse valor é em relação ao centro de gravidade, queremos o valor em relação ao fundo. Dessa força a coordena do centro de pressão é:
Agora, temos que montar a equação de momento.
Como estamos analisando o momento em que ela começa a se mexer, ou seja, o momento em que a comporta perde contato com o batente, a força nesse ponto é zero.
Vamos fazer o momento em relação ao ponto , assim agindo apenas duas forças a força interna e a força externa.
Feia, né? Vamos começar simplificando ela: Primeiro vamos fazer a multiplicação
Podemos dividir a equação por 2,5 e por 10.000 e assim teremos:
Agora, vamos dividir a equação por 9,8 e vamos obter:
E por fim, basta isolar , que encontramos:
Como queríamos o menor valor de que faça a comporta se movimentar, o menor valor é .