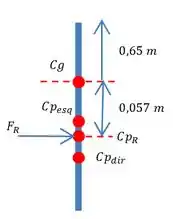
Encontre a linha de ação e o valor da força no portão circular da figura:
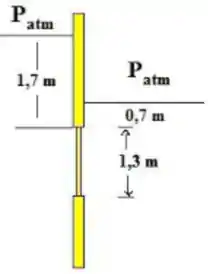
Passo 1
Agora, ao invés de termos um pressão fixa do lado externo igual na questão anterior, teremos de ambos os lados forças devido pressão causada pela coluna de fluido.
Para encontrarmos a força resultante basta primeiro encontrarmos a pressão resultante no centro de gravidade.
Assim, temos que
Encontrando a pressão resultante no centro de gravidade encontramos a força resultante.
A pressão no centro de gravidade é dada por:
O fluido é o mesmo dos dois lados. Assim o que vai influenciar diferenciar a pressão interna da externa será a profundidade do centro de gravidade.
Vamos começar calculando a pressão do lado esquerdo, região interna.
Como é uma placa plana e circular o centro de gravidade se encontra no meio da placa. Assim em .
Beleza, encontramos a pressão na região interna:
Já a pressão no lado direito será:
Agora vamos ver qual é a pressão resultante.
Como queremos a força, basta multiplicar pela área do portão. Tendo assim:
Passo 2
Beleza, agora vamos encontrar a linha de ação dessa força resultante. Mas pera!, o que seria a linha de ação de uma força??
Bem, é onde a força estaria virtualmente atuando, como se fosse o ponto onde aplicaríamos essa força resultante.
Por que isso? Bem, a força do lado esquerdo vai ser aplicada em um centro de pressão e a do outro lado será aplicada em outro centro de pressão.
E para gente achar o centro de pressão resultante teremos que fazer uma média ponderada com os centros de pressões onde os pesos serão as forças.
Estranho né? Vamos resolver o problema que você vai entender melhor.
Precisamos encontrar os centros de pressão de cada força.
Começando pelo lado esquerdo, temos:
Substituindo os valores que temos, chegamos em:
Olhando naquela tabela da teoria vemos que para um círculo:
Dessa forma:
Agora faremos o mesmo para encontrar o centro de pressão da pressão à direita.
Então chegamos na seguinte solução:
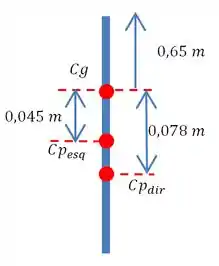
Bem, agora temos que encontrar a posição média do centro de pressão resultante. E para isso vamos fazer uma média ponderada. Onde o peso é a força em cada centro de pressão:
Usaremos o módulo das forças. E assim, temos:
Como essa posição representa um ponto abaixo do centro de gravidade deve ser colocado o sinal de negativo antes, sendo assim a posição em relação ao centro de gravidade:
Assim, temos que a força resultante irá aturar na posição: