Uma comporta plana semicircular , articulada ao longo de , é suportada pela força horizontal aplicada em . O líquido à esquerda da comporta é água. Calcule a força requerida para o equilíbrio.
Dados:
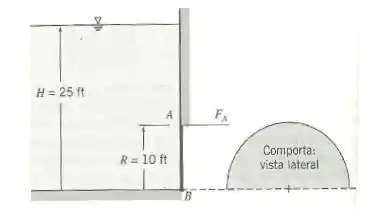
Passo 1
Essa questão é muito parecida com a anterior, o que vai mudar é que a comporta não é retangular. E isso vai influenciar na posição do centro de gravidade e no momento de inércia e, assim, mudar muitos valores. Mas o raciocínio para resolver é o mesmo.
Para resolvermos precisamos descobrir o valor da força causada pela pressão de água na comporta e o centro de pressão para podermos aplicar a equação de momento.
Passo 2
Vamos começar descobrindo a força de pressão.
Na teoria vimos que a força de pressão é dada por:
A densidade da água a gente sabe que é . A aceleração da gravidade é . E a profundidade do centro de gravidade a gente tem que calcular.
Para usarmos tudo em vamos transformar os valores que temos:
E:
Continuando agora, vamos calcular o centro de gravidade.
Bem, pra um semicírculo, o centro de gravidade é:
Mas a gente quer a profundidade e por isso temos que fazer a profundidade total do fluido menos a posição do centro de gravidade em relação ao fundo.
E por fim vamos calcular a área da comporta.
Podemos então calcular a força de pressão na comporta.
Passo 3
Agora vamos encontrar a posição do centro de pressão. Bem, estamos interessados só na posição , pois é dela que precisamos para aplicar a equação de momento.
Assim, na teoria vimos que a fórmula para encontrar o centro de pressão em relação ao centro de gravidade é:
O ângulo que a placa faz com a horizontal é e é:
A força de pressão a gente já calculou. Por fim falta apenas o momento de inércia da placa. Como é uma placa semicircular, o momento de inercia dessa figura:
Atenção. Aqui usamos o momento de inércia xx, que é o momento de inércia relativo à rotação em torno do eixo paralelo ao x que passa pelo centro de gravidade.
O Raio nós temos, então:
Jogando isso tudo na fórmula temos:
Lembrando que isso é em relação ao centro de gravidade, o que significa que a posição do centro de pressão é:
Então ficamos assim:
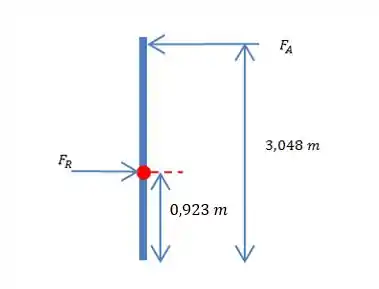
Beleza, agora podemos escrever a equação de momento, lembrando que as distâncias devem ser em relação ao ponto .
Isolando , temos: