Os cabos de sustentação eestão presos no topo da torre de transmissão. A força trativa no cabo vale . Determine a força trativa necessária no cabo , tal que o efeito resultante das duas trativas nos cabos seja uma força direcionada para baixo no ponto Determine o módulo dessa força.
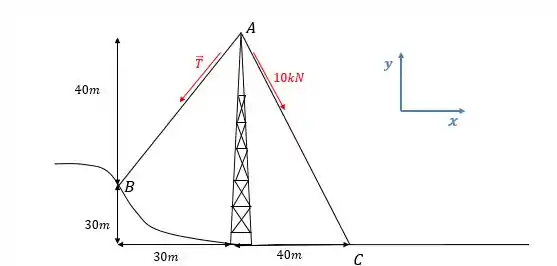
Passo 1
Primeiro vamos escrever as forças em componentes . Para isso, perceba que existem triângulos retângulos na figura que nos irão ajudar a achar os ângulos que as forças fazem com o eixo
Para força de , temos o triângulo:
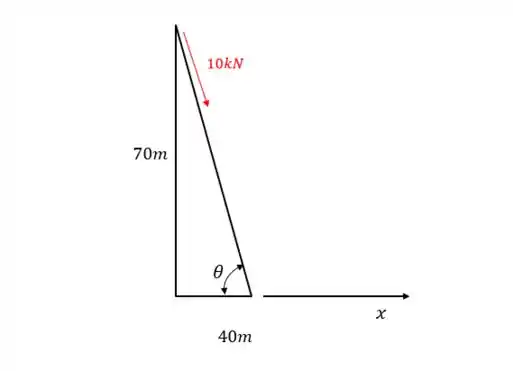
Assim, chamando a força de , ela poderá ser escrita como:
Perceba que eu coloquei o sinal de negativo, pois a força aponta para baixo, já que estamos analisando o ponto e ele está sendo puxado para baixo (chamamos isso de tração).
Pra achar o ângulo, basta fazermos:
Assim, a força será:
Passo 2
E a força Bom, nesse caso, o triângulo representativo que temos é:
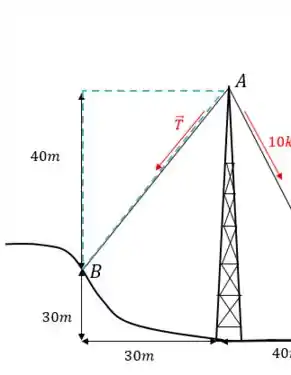
Ou seja:
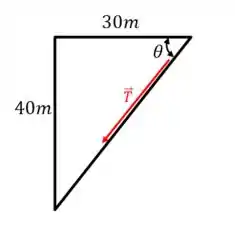
O ângulo vale:
E já que a tensão aponta no sentido negativo do eixo
Passo 3
Agora vem a parte que precisamos raciocinar mais: se a força resultante deve apontar apenas para baixo, ela não deve possuir uma componente na direção , certo?
Como vamos somar a força e a força de , podemos dizer a soma das componentes dessas forças em é nula:
E esse é o módulo da força necessária.
Passo 4
Para achar a resultante , basta a gente somar as componentes das forças:
E ela aponta para baixo, como era esperado!!!
O módulo dessa força vale:
Isso porque ela só possui uma componente.