Determine as componentes da força de ao longo dos eixos oblíquos e . Determine as projeções de sobre os eixos e
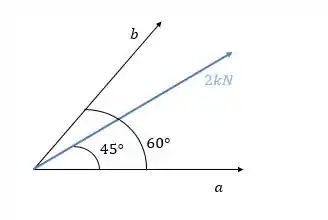
Passo 1
Vamos começar pela projeção mais fácil: A do eixo , Vamos lembrar que vamos projetar o vetor ao longo do eixo , como se fosse a sombra desse vetor.
Como sabemos exatamente qual é o ângulo que a força faz com o eixo , podemos simplesmente multiplicar a força pelo cosseno desse ângulo:
Isso pode ser mostrado visualmente como:
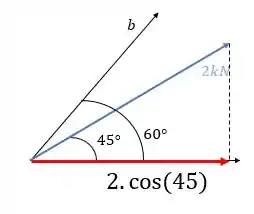
Essa força em vermelho é uma das componentes da força de ! Componente nada mais é do que dividir um vetor em outros eixos, olha só um caso geral:
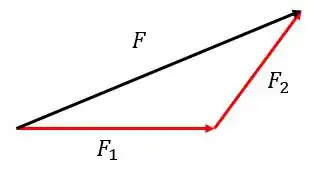
Aqui a força dividi-se em duas componentes e . Observe também que a soma dessas componentes é a própria força .
Passo 2
Já pra calcular a projeção da força no eixo , basta a gente perceber que o ângulo que a força faz com esse eixo vale
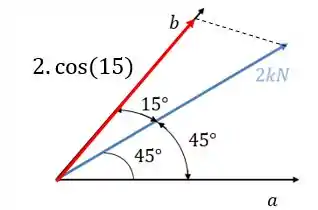
Podemos olhar também apenas as partes importantes para esse caso:
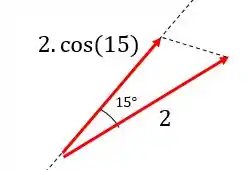
Afinal de contas, . Assim, podemos dizer que a projeção de no eixo vale:
Passo 3
Para achar as componentes, vamos usar a lei dos senos, já que os eixos não são os eixos
As componentes da força nas direções estão representadas abaixo:
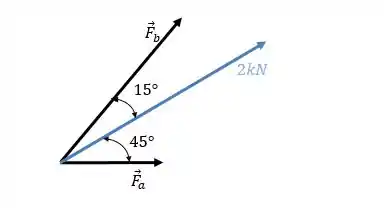
Perceba que componente e projeção são termos distintos, a soma das componentes sempre vai dar o vetor original!! Enquanto a soma das projeções (das sombras) irá dar um valor diferente da força (pelo fato dos eixos não serem perpendiculares)
Se deslocarmos o vetor (que é a componente de em ), mantendo a sua direção e sentido, formamos o seguinte triângulo:
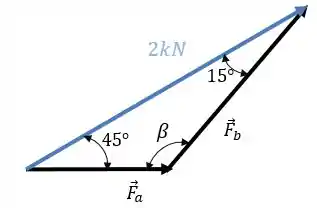
Não sabemos quanto vale , mas como a soma dos ângulos internos de um triângulo é sempre igual a
Assim:
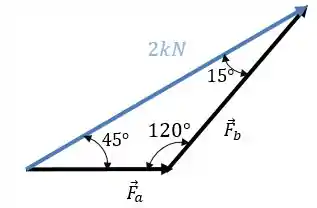
Pela lei dos senos:
Assim: