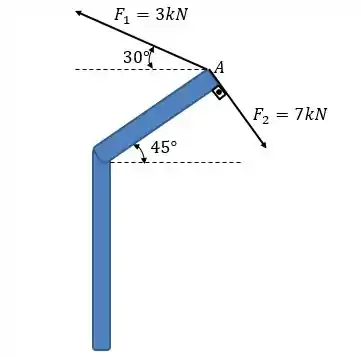
As duas forças mostradas atuam no ponto da barra dobrada. Determine a resultante das forças.
Passo 1
Nessa questão você quer saber a resultante das forças que atuam em , ou seja, a soma das forças.
A forma mais fácil de se fazer isso, novamente, é pela soma das componentes das forças. Então, nosso primeiro trabalho vai ser escrever essas forças em termos de vetores
Passo 2
Vamos analisar primeiro a força de
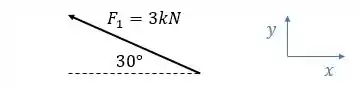
A força faz um ângulo de com o sentido negativo do eixo ( o que corresponderia a com o sentido positivo do eixo).
Assim, a componente horizontal do vetor será negativa. Podemos dizer que a força pode ser escrita por:
Passo 3
Agora vamos olhar para a força de o ângulo que ela faz com o eixo positivo não está explicito, mas podemos calculá-lo:
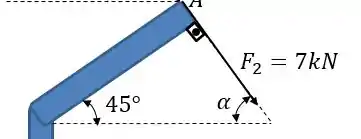
A soma dos ângulos internos de um triângulo tem que dar , certo? Então:
Assim, o ângulo vale . Perceba que: a força aponta para baixo, logo, a componente vertical é negativa.
Ela aponta para frente, logo a componente horizontal é positiva.
Assim:
Passo 4
A resultante será: