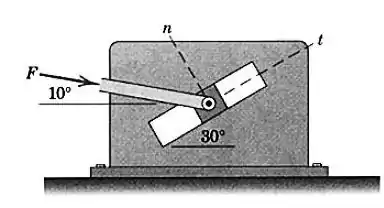
O componente da força vale . Determine o componente (normal) e o módulo de
Passo 1
O sistema de forças pode ser representado por:
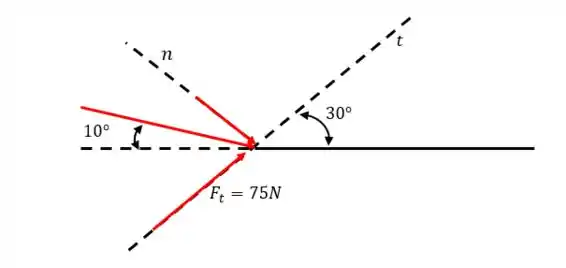
Nós só sabemos quanto vale a componente tangencial da força e queremos saber quanto vale a componente normal e o módulo da força total.
Passo 2
Vamos analisar os ângulos:
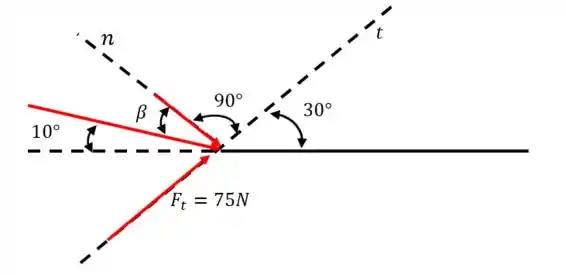
Não sabemos quanto vale , mas como a soma dos ângulos na figura tem que ser igual , podemos dizer que:
Passo 3
Agora, se arrastarmos o vetor tangencial, podemos formar o seguinte triângulo:
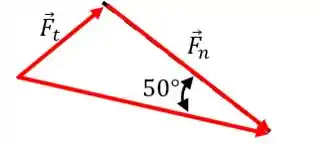
Pela definição de tangente, podemos escrever:
E a direção? Pela figura, a componente normal está orientada no sentido negativo do eixo normal. Assim:
Passo 4
De novo no triângulo anterior, perceba que a relação entre o módulo da força e o módulo da componente normal é dada por:
Resposta
Exercícios de Livros Relacionados
183- Um dos problemas críticos no projeto de veículos para mergulhos profundos é colocar visores que irão suportar pressões hidrostáticas tremendas sem fraturar ou vazar. A figura mostra a seção trans
Determine a intensidade da força resultante e sua direção, medida no sentido anti-horário a partir do eixo x positivo.
Uma força F de módulo 800N é aplicada ao ponto C da barra A B , como mostrado. Determine os componentes x - y e n - t de F .
Determine o módulo F s da força trativa atuando na mola, para que a resultante de F s e de F seja uma força vertical. Determine o módulo R dessa força resultante vertical.
Um cabo esticado entre os suportes fixos A e B está sob uma tração T de 900N . Usando os vetores unitários i e j expresse a tração como um vetor; primeiramente como uma força T A atuando em A e, em se