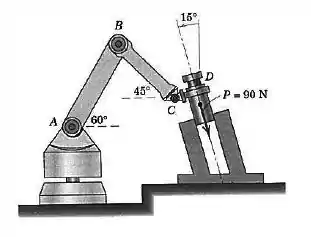
No projeto de um robô para colocar, sem folga, a pequena parte cilíndrica em um furo circular, o braço deve exercer uma força de na peça, paralelamente ao eixo do furo, como mostrado. Determine as componentes da força que a peça exerce sobre o robô ao longo dos eixos paralelo e perpendicular ao braço e paralelo e perpendicular ao braço .
Passo 1
Essa questão vai nos dar um pouco mais de trabalho. O primeiro passo é perceber o que está sendo pedido: as componentes normais e tangenciais em cada trecho.
a)
Vamos desenhar dois triângulos que vão nos ajudar quais são os ângulos que a força faz com os eixos do trecho
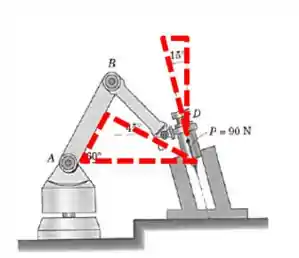
Agora vamos olhá-los separadamente, marcando os eixos e a força:
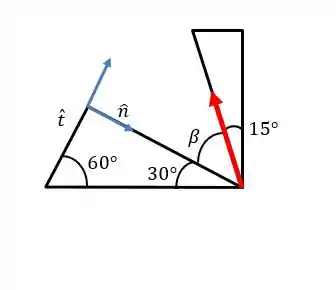
Perceba que o ângulo de está ali porque o primeiro triângulo é retângulo, assim como o segundo.
Outra coisa: Percebeu que a força tem o sentido contrário da força do enunciado? Isso acontece porque estamos analisando a força que a peça faz na estrutura, ou seja, é a reação da força do enunciado.
Passo 2
Para decompor a força, precisamos descobrir quanto vale o ângulo . Olhando a figura do passo anterior, dá para ver que a soma dos ângulos tem que dar , assim:
Agora ficou fácil:
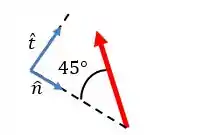
Podemos escrever a força como:
Passo 3
b):
Bora desenhar os triângulos na figura de novo:
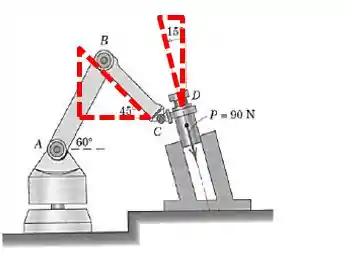
Analisando os triângulos separadamente e marcando a força e os eixos:
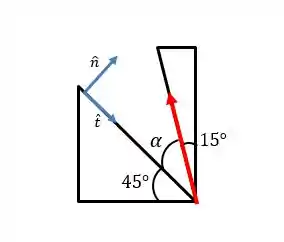
Quanto vale Já sabe, só se ligar que a soma dos ângulos tem que dar
Passo 4
Agora ficou fácil! Só fazer a decomposição usando o ângulo:
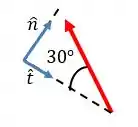
Assim:
Resposta
a)
b)