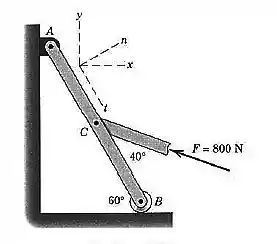
Uma força de módulo é aplicada ao ponto da barra , como mostrado. Determine os componentes e de
Passo 1
Precisamos descobrir quais são os ângulos que a força de faz com os eixos e.
Para isso, vamos ter que usar um pouco de geometria, como fizemos antes.
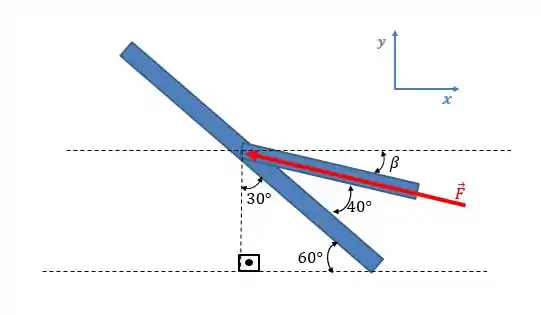
Vamos interpretar o desenho: o triângulo inferior tem dois ângulos agudos: e. O ângulo de foi dado no enunciado e o de foi calculado levando-se em consideração que o triângulo é retângulo:
Mas o ângulo que nos interessa é o ângulo . Para calculá-lo, basta você perceber que a soma dos ângulos de , e tem que dar . Assim:
Passo 2
Com esse ângulo, fica fácil descobrir as componentes
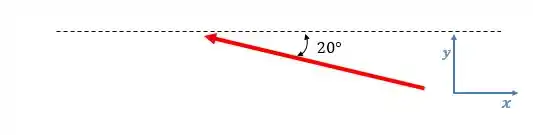
Assim, as componentes e , em módulo, serão:
Como dá pra ver pelo vetor, a componente aponta no sentido contrário do eixo . Assim, podemos escrever a força como:
Passo 3
E as componentes tangencias e normais? Essas são mais fáceis nesse problema pois o ângulo de é tudo que precisamos:
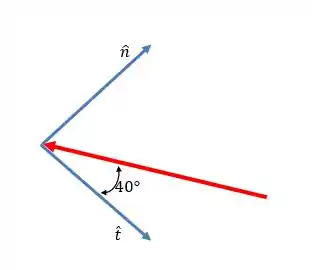
Assim:
E os sentidos? Dá para ver, pela figura, que ambas as componentes são contrárias aos sentidos positivos dos eixos. Assim, a força pode ser escrita assim: