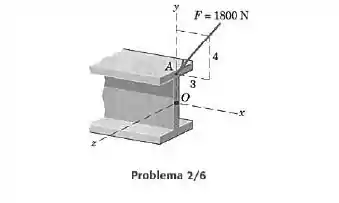
A força de é aplicada à extremidade da viga em Expresse como um vetor em termos de e j.
Passo 1
Podemos fazer da seguinte forma: Vamos calcular qual é o ângulo que a força faz com o eixo Depois vamos calcular as componentes escalares e e, por fim, escrever a força em função delas e dos vetores unitários.
Passo 2
O enunciado nos deu uma figura e, nessa figura, existe um triângulo. O ângulo que a força faz com o eixo é semelhante ao ângulo que o triângulo possui:
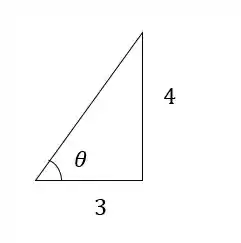
A tangente desse ângulo vale:
Assim, o ângulo vale:
Passo 3
Agora podemos calcular o módulo das componentes da força nos eixos (perceba que tais componentes estão orientadas no sentido negativo de seus eixos):
Passo 4
Assim: