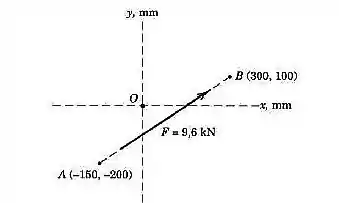
A linha de ação da força de passa pelos pontos , como mostrado na figura. Determine os componentes escalares e de
Passo 1
Primeiro vamos descobrir quem é o vetor que representa a direção . Para isso, vamos subtrair as coordenadas dos dois pontos:
Passo 2
Nosso próximo passo é achar o módulo deste vetor, ou seja, o seu tamanho. Para isso, temos que:
Passo 3
Agora vamos normaliza-lo! Isso vai ser importante na etapa de representação da força e, além disso, vai nos dar um vetor adimensional e unitário que representa a direção. Para isso, vamos dividir o vetor pelo seu módulo:
Passo 4
Agora, podemos escrever a força multiplicando-a pelo vetor normalizado:
Perceba que eu coloquei a força em Newtons, não em
Assim, os componentes escalares são: