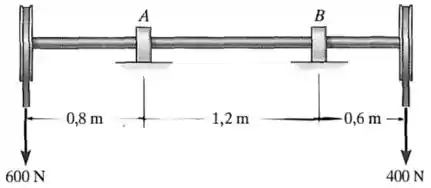
Determine o menor diâmetro admissível do eixo que está sujeita às forças concentradas. Os mancais de luva em e suportam somente forças verticais, e a tensão de flexão admissível é .
Passo 1
O que é que o exercício quer?
Ele quer saber qual é o menor diâmetro que o eixo circular pode ter de tal forma que a tensão de flexão no eixo não ultrapasse em módulo o seu valor admissível .
Ou seja, ele quer saber qual é o menor diâmetro que respeita a condição:
Então para resolver essa questão, precisamos saber descrever em função do diâmetro do eixo.
E como podemos fazer isso?
Bom, para descrever , precisamos avaliar os valores de de acordo com a fórmula da flexão:
Onde:
- (ou alternativamente, só “”) é o momento fletor em uma seção do eixo;
- é a posição de um ponto da seção do eixo em relação à sua linha neutra;
- & (ou alternativamente, só “”) é o momento de inércia da área da seção transversal desse eixo.
Mas olha só...
Primeiro, o momento fletor máximo absoluto “” nesse eixo pode ser encontrado a partir dos métodos da estática (DCL, equilíbrio, análise dos esforços internos & diagramas de esforços internos).
Segundo, a linha neutra de um eixo circular fica bem no meio do eixo, e, então, o valor máximo absoluto de vai corresponder ao raio do eixo:
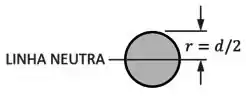
E terceiro, o momento de inércia da área de uma seção transversal circular é:
Que ainda pode ser expressa em função do diâmetro do eixo como:
Então pode ser definido como:
O que simplificando, fica assim:
Então resumindo tudo...
Para resolver esse exercício, precisamos aplicar os métodos da estática para determinar o momento fletor máximo absoluto nesse eixo.
Feito isso, vamos conseguir descrever a tensão máxima absoluta no eixo em função do diâmetro .
E, em seguida, vamos poder usar isso e a condição de projeto para descobrirmos os diâmetro necessário para o nosso eixo.
Passo 2
Então vamos lá!
![]()
Começando pelo primeiro passo dos métodos da estática, nós temos o DCL ou:
![]()
O exercício já falou que os apoios em e só realizam reações na vertical, então nosso DCL fica assim:
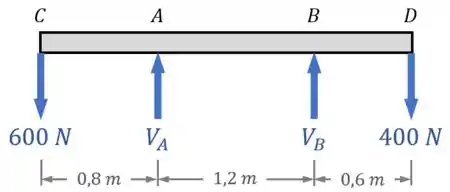
Passo 3
Próximo passo é o:
![]()
Aplicando no nosso eixo o equilíbrio de forças na vertical, nós vamos ter que:
O que significa que:
Por outro lado, aplicando o equilíbrio de momentos em relação ao ponto , temos:
Isolando e calculando o restante, temos que:
O que significa que:
Por fim, substituindo esse valor na expressão anterior , encontramos que:
E assim finalizamos toda a análise dos esforços externos no nosso eixo!
![]()
Passo 4
Com isso, podemos seguir para o terceiro passo dos métodos da estática, que é a:
![]()
Existem descontinuidades (nesse caso, forças concentradas) nos pontos , , e da nossa viga.
Então devemos observar os esforços internos nas seções entre e , entre e e entre e :
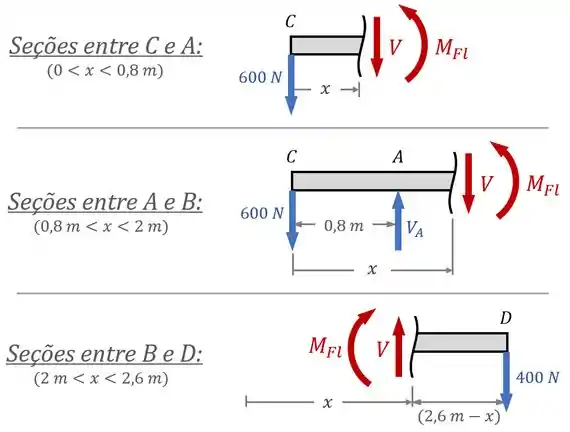
Aí, como nesse exercício queremos analisar o momento fletor máximo absoluto no eixo, vamos focar em determinar os momentos fletores no eixo, pulando o cálculo das forças cortantes .
Para as seções as seções entre e , o equilíbrio de momentos em relação ao ponto da seção nos diz que:
O que significa que:
Em seguida, para as seções entre e , temos:
Substituindo e isolando , temos:
Fazendo a distributiva, isso fica assim:
O que significa que:
Por fim, para as seções entre e , temos:
Isolando , temos:
E fazendo a distributiva, encontramos que:
Passo 5
Finalmente, chegamos no último passo dos métodos da estática, que são os:
![]()
Aqui, só precisamos fazer um diagrama para o momento fletor da viga, que é descrito por 3 equações de primeiro grau de :
Pela primeira equação, o momento fletor varia linearmente de para .
Pela segunda, ele varia linearmente de para .
E pela terceira, ele varia linearmente de para .
Dessa forma, o diagrama do momento fletor fica assim:
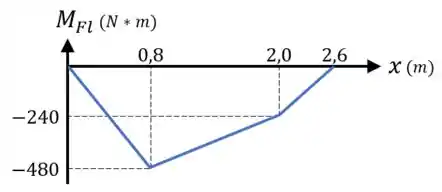
E tcharam!
![]()
Desse diagrama conseguimos identifica que o momento fletor máximo absoluto no nosso eixo é:
Passo 6
Agora, podemos seguir o exercício aplicando a nossa condição:
Aplicando a fórmula da flexão para a determinação da tensão máxima absoluta no eixo, temos que:
De tal forma que a nossa condição pode ser reescrita assim:
Em seguida, substituindo:
- ;
- & ,
...e simplificando tudo, a nossa condição fica assim:
E isolando , temos:
Aí, substituindo os valores:
- ,
- & ,
...e não se esquecendo de fazer a raíz cúbica, encontramos que:
O que significa que o diâmetro mínimo necessário para o eixo é: