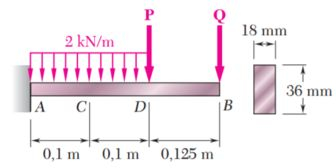
A viga suporta uma força uniformemente distribuída de e duas forças concentradas e . Foi determinado experimentalmente que a tensão normal provocada pelo momento fletor na borda inferior da viga fosse de em e de em . Trace os diagramas de força cortante e momento fletor para a viga, e determine a intensidade das forças e .
Passo 1
O que está acontecendo?
Devido ao carregamento nessa viga, existem ao longo dela esforços internos na forma de forças cortantes e momentos fletores .
Devido a esses momentos fletores , surgem ao longo da viga tensões normais de tração () e compressão () de acordo com a fórmula da flexão:
Onde:
- (ou só “”) é o momento fletor em uma seção transversal da viga;
- é a posição do ponto da seção em que se quer calcular a tensão em relação à linha neutra da seção;
- & (ou só “”) é o momento de inércia da área da seção.
Aí...
O exercício nos diz que na borda inferior da viga, nos pontos em que a posição em relação à linha neutra :
...a tensão na seção é:
...enquanto que a tensão na seção é:
Sendo que como a seção transversal dessa viga é simétrica, a sua linha neutra fica bem no meio da seção:
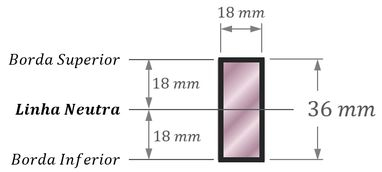
O que significa que a posição em relação à linha neutra dos pontos da borda inferior é:
E além disso, o momento de inércia da área dessa seção transversal retangular de base e altura pode ser calculado pela fórmula:
O que tudo isso significa é que...
Aplicando a fórmula da flexão para a borda inferior das seções e , vamos conseguir descobrir o valor do momento fletor nessas seções.
E o que é que o exercício quer?
Ele quer saber o valor das forças e desconhecidas na viga.
Então, o que a gente pode fazer é:
1. Utilizar os métodos da estática (DCL, equilíbrio e análise dos esforços internos) para descobrir o valor do momento fletor nas seções e da viga em função das forças e .
2. Aplicar a fórmula da flexão para a borda inferior das seções e para encontrar o valor do momento fletor nas seções e .
& 3. Igualar os resultados para o momento fletor em e obtidos pelo primeiro e pelo segundo método para podermos isolar e encontrar os valores das forças e .
Ao final, o exercício ainda pede que a gente faça os diagramas de força cortante e de momento fletor para essa viga.
Passo 2
Então vamos começar com o primeiro passo dos métodos da estática, que é o DCL ou:
![]()
Para essa viga, o engaste em vai realizar:
- Uma reação na horizontal, ; (que vai acabar sendo nula e pode ser omitida do DCL)
- Uma reação na vertical, ;
- E um momento .
Dessa forma, o nosso DCL vai ficar assim:
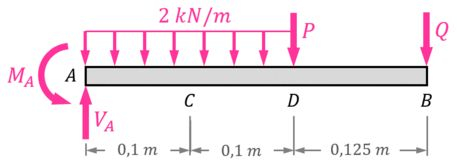
Passo 3
Feito o DCL, seguimos para o:
![]()
Aplicando o equilíbrio de forças na vertical, vamos ter:
Na hora de fazer esse somatório, consideramos a força distribuída uniforme de que atua ao longo do comprimento de da viga como uma força equivalente:
Dessa forma, o nosso somatório de forças na vertical fica assim:
O que significa que:
Sendo que esse resultado está em .
Em seguida, podemos aplicar o equilíbrio de momentos em relação ao ponto :
Aqui, como a força distribuída de é uniforme, podemos considerar que a sua força equivalente de atua no ponto , bem no meio do comprimento .
Sabendo disso e considerando os momentos no sentido anti-horário como positivo (), o nosso somatório de momentos fica assim:
Isolando , encontramos que:
Sendo que esse resultado está em .
Passo 4
Encontrados os valores dos esforços externos atuantes na nossa viga, seguimos para a:
![]()
Nessa viga, temos descontinuidades:
- em ; (início da viga, início de uma força distribuída, força concentrada e momento concentrado)
- em ; (fim de uma força distribuída e força concentrada)
- & em . (final da viga e força concentrada)
Então precisamos avaliar as seções entre e & as seções entre e :
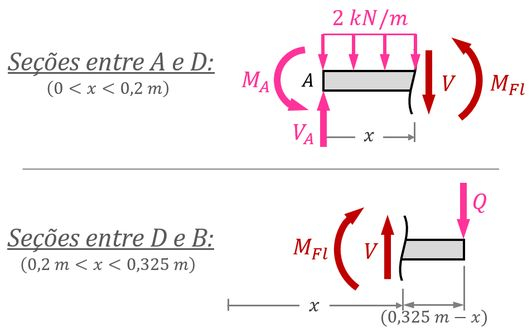
Feitos esses desenhos, precisamos aplicar as condições de equilíbrio em cada caso.
Primeiro, observamos as seções entre e .
Aplicando o equilíbrio de forças na vertical, temos:
Aqui, a força distribuída uniforme de que atua ao longo do comprimento pode ser considerada como uma força equivalente .
Dessa forma, o nosso somatório de forças fica assim:
Substituindo e isolando , encontramos que:
Sendo que esse resultado está em !
Em seguida, aplicando o equilíbrio de momentos em relação ao ponto da seção, temos:
Aqui, como a força distribuída de é uniforme, podemos considerar que a sua força equivalente de atua bem no meio do pedaço de viga que estamos estudando.
Sendo assim, o nosso somatório de momentos fica assim:
Substituindo e , temos:
Isolando , encontramos que:
Sendo que esse resultado está em !
Em seguida, observamos as seções entre e .
Aplicando o equilíbrio de forças na vertical, temos que:
O que significa que:
Já aplicando o equilíbrio de momentos em relação ao ponto da seção, temos:
Fazendo a distributiva, temos:
Por fim, isolando , encontramos que:
Sendo que esse resultado está em !
E assim finalizamos a nossa análise dos esforços internos!
Passo 5
Agora, já podemos determinar quais são os momentos fletores nas seções e da viga em função das forças e .
Tanto a seção quanto a seção estão entre e .
Dessa forma, os momentos fletores nessas seções vão ser descritos pela fórmula:
Para a seção , temos que , de tal forma que:
Já para a seção , temos que , de tal forma que:
Desenvolvendo essa expressão, temos:
E, simplificando isso, encontramos que:
Lembrando que esses resultados para o momento fletor estão em !
Passo 6
Em seguida, precisamos encontrar os momentos fletores pelo segundo método, que é aplicando a fórmula da flexão para as bordas inferiores das seções e .
Aplicando a fórmula da flexão, temos:
Primeiramente, para a borda inferior da seção , vamos substituir:
- ;
- ;
- ;
- & ,
- ;
- ;
- ;
- & ,
De tal forma que:
Isolando , temos que:
Simplificando isso, encontramos:
O que dá:
Agora, como o resultado que encontramos para pelos métodos da estática estão em , vamos converter esse resultado também para , obtendo que:
Depois, para a borda inferior da seção , substituímos:
De tal forma que:
Isolando e simplificando tudo, encontramos que:
O que dá:
Passo 7
Determinados os valores de e pelos dois métodos e estando tudo em , podemos igualar agora esses valores.
Primeiro, para , temos:
Isolando , encontramos que:
Já para , temos:
Substituindo , isso fica assim:
Fazendo a distributiva:
Simplificando:
Isolando , encontramos que:
Inserindo esse resultado em , temos:
Ou seja, temos que:
Passo 8
Aqui, praticamente já resolvemos o exercício: só falta fazermos os:
![]()
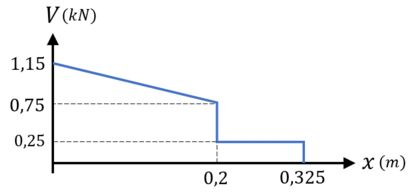
Para a força cortante , temos que:
Primeiro, ela é descrita pela equação no trecho .
Substituindo e , essa equação fica assim:
O que significa que a força cortante varia linearmente entre os pontos e .
Depois, ela é dada por no trecho .
Dessa forma, o diagrama da força cortante fica assim:
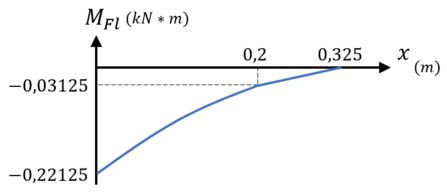
Já para o momento fletor , temos que:
Primeiro, ele é descrito por:
...no trecho .
Substituindo e , essa equação fica assim:
O que significa que o momento fletor varia parabolicamente, com uma concavidade para baixo (uma vez que a segunda derivada da função acima é negativa), entre os pontos:
Além disso, fazendo a primeira derivada dessa função e igualando-a a zero, encontramos que o seu ponto crítico é , o que está fora do trecho .
Em seguida, ele é descrito por:
...no trecho .
Substituindo , isso fica assim:
O que significa que varia linearmente entre os pontos:
Dessa forma, o nosso diagrama de momento fletor fica assim:
E assim terminamos o nosso exercício!