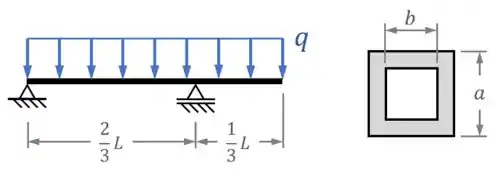
A viga da figura abaixo possui um comprimento total , está submetida a uma carga uniformemente distribuída e possui uma seção transversal na forma de um tubo quadrado, com lados externos de comprimento e lados internos de comprimento .
Determine a tensão de flexão máxima nessa viga e faça um rascunho da distribuição de tensões na seção transversal da viga onde ocorre essa tensão máxima.
Passo 1
O que está acontecendo?
A carga distribuída uniformemente e as reações realizadas pelos apoios nessa viga vão gerar nela esforços internos na forma de forças cortantes e momentos fletores .
Em uma ou mais seções transversais dessa viga, o momento fletor vai ter o seu valor máximo absoluto.
Nessas seções de momento máximo, vão ocorrer as tensões de flexão máximas na viga, de acordo com a fórmula da flexão:
Onde:
- (ou só “” para alguns professores) é o momento fletor na seção transversal;
- é a posição do ponto da seção transversal em que se quer avaliar a tensão em relação à linha neutra da seção;
- & (ou só “” para alguns professores) é o momento de inércia da área da seção.
E o que é que o exercício quer?
Ele quer que a gente determine a maior tensão de flexão causada nessa viga em função das variáveis , , e que ele indicou no enunciado.
Então...
Para resolver esse exercício, temos que:
1. Encontrar o momento fletor máximo em termos absolutos nessa viga.
Para tanto, devemos usar os métodos da estática: DCL, equilíbrio, análise dos esforços internos & diagramas de esforços internos.
2. Analisar a geometria da seção transversal dessa viga para encontrar a posição de sua linha neutra e o seu momento de inércia da área .
Aqui, como a seção dessa viga é simétrica em relação à horizontal, já podemos afirmar que a sua linha neutra possui uma posição média :
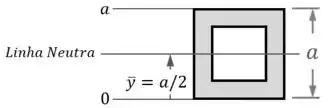
Além disso, também vemos que os maiores valores da posição de um ponto dessa seção transversal em relação à linha neutra são para o topo da seção e para a base.
Dessa forma, só falta calcular para essa seção o momento de inércia da área .
& 3. Aplicar a fórmula da flexão para os valores máximos absolutos de e , encontrando assim a tensão de flexão máxima nessa viga, resolvendo o exercício.
Ao final, o exercício ainda pede que a gente aproveite os resultados obtidos para fazer um rascunho da distribuição de tensões na seção transversal da viga onde ocorre essa tensão máxima.
Passo 2
Então vamos começar pelo primeiro passo dos métodos da estática, que é o DCL ou:
![]()
Para essa viga:
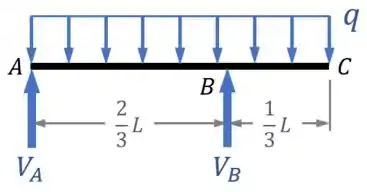
- O apoio móvel à direita vai realizar uma reação na vertical ;
- E o apoio fixo na extremidade esquerda vai realizar uma reação na horizontal (que vai acabar sendo nula e pode ser omitida do DCL) e uma reação na vertical .
Dessa forma, o nosso DCL fica assim:
Passo 3
Feito o DCL, seguimos para o:
![]()
Aplicando o equilíbrio de forças na vertical, temos:
Na hora de fazer esse somatório, consideramos a força uniformemente distribuída que atua ao longo do comprimento total da viga como uma força equivalente .
Dessa forma, o somatório fica assim:
O que significa que:
Em seguida, podemos aplicar o equilíbrio de momentos em relação ao ponto da viga:
Aqui, como a força distribuída é uniforme, nós temos que a sua força equivalente atua bem no meio da viga.
Dessa forma, a força equivalente vai ter um braço em relação ao ponto .
Sabendo disso, podemos fazer o somatório de momentos acima, que fica assim:
Isolando , temos que:
Cortando com e depois isolando , encontramos que:
Por fim, podemos substituir esse valor na expressão anterior e isolar para encontrar que:
Passo 4
Agora, já conhecemos os valores dos esforços externos atuantes na nossa viga.
Então podemos seguir agora para a:
![]()
Nessa viga, temos descontinuidades em , e , então precisamos avaliar as seções entre e e as seções entre e :
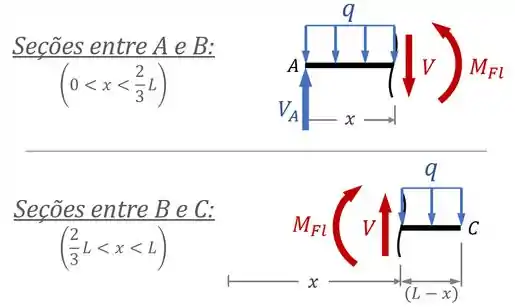
Aí, para finalizar a análise dos esforços internos, devemos aplicar as equações de equilíbrio em cada situação para descobrirmos os valores dos esforços internos e nas diferentes seções da viga.
Mas no caso desse exercício...
Ele só quer descobrir as tensões de flexão máximas, que são causadas pelo momento fletor .
Então só precisamos aplicar o equilíbrio de momentos em relação ao ponto da seção em cada situação para descobrirmos os valores de .
Para as seções entre e , vamos ter:
Olhando para o desenho acima do pedaço de viga para as seções entre e , vemos que a força uniformemente distribuída atua ao longo do comprimento desse pedaço de viga.
Assim, concluímos que ela vai atuar como uma força equivalente com um braço em relação ao ponto da seção.
Percebendo como nesse caso, somente o momento gerado pela força vai estar no sentido horário (), o nosso somatório de momentos fica assim:
Substituindo , temos:
Em seguida, isolando , encontramos que:
Já para as seções entre e , temos:
Dessa vez, a força distribuída vai atuar como uma força equivalente com um braço em relação ao ponto da seção.
Percebendo como, nesse caso, tanto o momento fletor quando o momento gerado por estão no sentido horário (), o nosso somatório de momentos fica assim:
Isolando , encontramos que:
Desenvolvendo o termo , temos:
Finalmente, fazendo a distributiva, conseguimos indicar a função que expressa o momento fletor nas seções entre e em função da posição que está sendo avaliada:
Passo 5
Por fim, podemos seguir para o último passo dos métodos da estática, que são os:
![]()
No passo anterior, vimos que o momento fletor é descrito por duas funções.
Primeiro, vimos que para o trecho , o momento fletor é dado por:
Analisando essa função, podemos observar que:
- A sua segunda derivada é negativa. Assim podemos concluir que essa função quadrática possui uma concavidade virada para baixo.
- O seu ponto crítico (aquele em que a sua primeira derivada é igual à zero) ocorre em .
- E que, como ela possui uma concavidade para baixo, esse ponto crítico é um ponto de máximo para a função.
Além disso, podemos calcular o valor do momento fletor no ponto :
No ponto de máximo :
E no ponto :
Em seguida, para o trecho , o momento fletor é dado por:
Analisando essa função, observamos:
- Que ela possui uma concavidade para baixo, uma vez que a sua segunda derivada é negativa;
- Que o seu ponto crítico (aquele em que a sua primeira derivada é igual à zero) ocorre em ;
- E que, como essa função possui uma concavidade para baixo, esse ponto crítico é um ponto de máximo.
Além disso, podemos calcular o momento fletor no ponto :
O que vai dar:
E podemos calcular o momento fletor no ponto de máximo :
Que vai dar:
Assim...
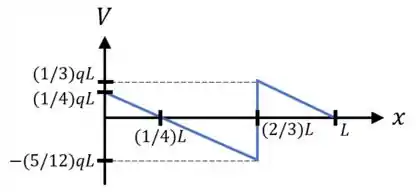
Usando todos esses pontos e conhecendo a concavidade dessas curvas, conseguimos desenhar o diagrama de momento fletor para essa viga:

E, desse diagrama de momento fletor, conseguimos retirar que o momento fletor máximo nessa viga em termos absolutos é:
Além disso...
Para resolver esse exercício, não é necessário fazer o diagrama da força cortante na viga.
Mas mesmo assim, muitos professores pedem que esse diagrama seja sempre feito.
Então, caso você queira fazer esse diagrama em casa e comparar os resultados, ele fica assim:
Passo 6
Agora, vamos estudar as propriedades geométricas da seção transversal dessa viga.
No passo 1, nós já vimos que a posição da linha neutra da seção transversal dessa viga é , uma vez que a seção transversal é simétrica em relação à horizontal.
Então só nos resta calcular o:
![]()
Para calcular o momento de inércia da área da seção transversal dessa viga, devemos observar a sua geometria:
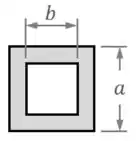
Em seguida, devemos separar essa geometria em elementos numerados.
Aqui, nós temos duas opções:
A primeira opção é separar a geometria da seção em 4 retângulos numerados:
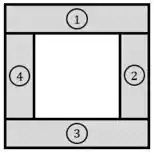
Mas essa opção vai resultar em cálculos desnecessariamente complicados.
Já a segunda opção é separar a geometria em um quadrado maior de lado (elemento na figura abaixo) e um furo na forma de uma quadrado menor de lado (elemento na figura):
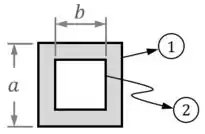
Sendo que, nessa segunda opção, precisamos considerar o elemento que é um furo como um elemento de momento de inércia da área negativo e de área negativa.
A segunda opção facilita os cálculos, então vamos escolher ela!
Definidos os elementos que compõem a geometria da nossa seção, devemos calcular em seguida o momento de inércia da área de cada elemento.
No nosso caso, tanto o elemento quanto o elemento são quadrados.
Dessa forma, podemos usar para eles a fórmula do momento de inércia da área de um retângulo:
Para o elemento , um quadrado de lado , nós vamos ter uma base e uma altura , de tal forma que:
Já para o elemento , um quadrado de lado , vamos ter uma base e uma altura .
Lembrando que o elemento é um furo e, portanto, deve ter um valor de negativo, o seu momento de inércia da área fica assim:
Em seguida, como os elementos e da nossa seção já estão centrados na linha neutra da seção, não precisamos usar o teorema dos eixos paralelos.
Assim, o momento de inércia da área da seção transversal como um todo vai ser dado pela soma:
Substituindo os valores de e , vamos ter:
O que significa que:
Passo 7
Finalmente, podemos calcular a tensão de flexão máxima na nossa viga.
Aplicando a fórmula de flexão, temos:
Aí, sabendo que a tensão máxima na viga vai ocorrer:
- Na seção em que o momento fletor tem seu valor máximo em termos absolutos ;
- E nos pontos em que tem seus valores máximos em termos absolutos, que são no topo da seção da viga, onde , e na base da seção, onde ,
E substituindo , encontramos que as tensões máximas na nossa viga vão ser:
Simplificando essa expressão, temos:
E, como , isso significa que:
Sendo que o valor positivo, de tração, ocorre o no topo da seção da viga, onde , e o valor negativo, de compressão, ocorre na base, onde .
(Isso porque o nosso momento fletor é negativo. Caso ele fosse positivo, o contrário ocorreria!)
Aí, para fornecer a nossa resposta final, podemos indicar somente o valor absoluto:
E assim encontramos a nossa resposta para o exercício!
Passo 8
Por último, o exercício ainda quer que a gente faça um rascunho da distribuição de tensões na seção onde ocorre essa tensão .
Então vamos pensar...
Definindo uma coordenada começando na base da seção da viga:
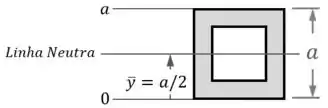
...vamos ter que:
- Na base da seção, na posição , a tensão vai ser igual a , como acabamos de ver no passo anterior;
- No topo da seção, de posição , ela vai ser igual a , também como acabamos de ver;
- E no centro da seção, de posição , onde há a linha neutra de tal forma que a posição da fórmula da flexão vai ser nula, a tensão vai ser nula.
Aí, marcando esses pontos em um gráfico, e ligando eles por uma reta, vamos ter o nosso rascunho da distribuição de tensões na seção:
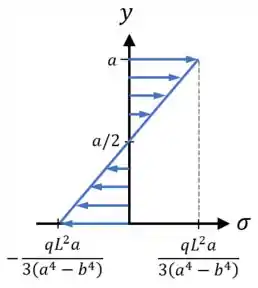
E assim terminamos de vez o exercício!