A viga é composta por três tábuas de madeira pregadas como mostra a figura. Se o momento que age na seção transversal for , determine a tensão de flexão máxima na viga. Faça um rascunho da distribuição de tensão que age na seção transversal.
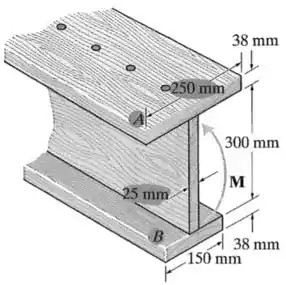
Dica do Expert: Determine a posição da linha neutra da viga, depois calcule o momento de inércia da área da viga, e, por último, aplique a fórmula da flexão.
Passo 1
O que está acontecendo?
O momento aplicado vai gerar na seção transversal da viga uma tensão normal de flexão que é descrita pela fórmula da flexão:
Onde:
- (ou ) é o momento fletor aplicado na seção transversal;
- é a posição ponto onde se quer calcular a tensão de flexão em relação à linha neutra (ou eixo neutro) da viga;
- & (ou ) é o momento de inércia da área da seção transversal da viga em relação à sua linha neutra.
E o que é que o exercício quer?
Ele quer que a gente determine a tensão de flexão máxima nessa viga.
Então...
Para resolver o exercício, nós vamos ter que:
1. Determinar a posição da linha neutra.
Para fazer isso, podemos fazer uma média das posições dos centros de cada tábua de madeira ponderadas de acordo com as áreas de cada tábua:
Sendo que uma das formas de identificar os termos e dessa equação consiste em numerar cada tábua da viga e preencher uma tabela como a da figura abaixo:
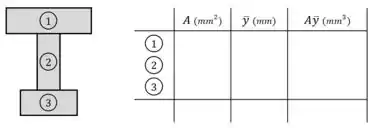
Feito isso, podemos seguir para os próximos passos, que são:
2. Calcular o momento de inércia da área para essa viga.
Para fazer isso, vamos ter que nos lembrar:
- Que o momento de inércia da área de cada tábua retangular é , onde é a base da tábua (paralela à linha neutra) e é a sua altura (perpendicular à linha neutra);
- E que, devido ao teorema dos eixos paralelos, o momento de inércia da área da viga vai ser:
Onde é a distância do centro de cada tábua até a linha neutra .
& 3. Indicar o valor máximo absoluto de e calcular a tensão de flexão máxima absoluta, resolvendo assim o exercício.
Sendo que o valor máximo de vai ocorrer sempre ou para o topo ou para a base da viga.
Ao final de tudo, o exercício ainda quer que a gente faça um rascunho da distribuição de tensão que ocorre na seção transversal da viga.
Então sim... Eu sei... Parece muita coisa.

Mas segura aí que você consegue! 👊
Passo 2
Então vamos começar determinando a posição da linha neutra.
Para tanto, temos que olhar para a figura original do exercício:
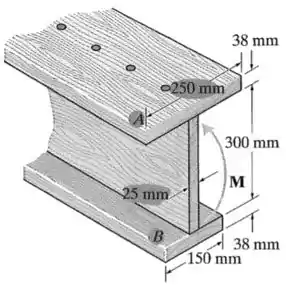
Numerar as 3 tábuas da viga e identificar a base da viga como a posição :
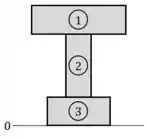
E preencher, em uma tabela, o valor das áreas e das posições dos centros de cada tábua, além do produto desses valores para cada tábua:
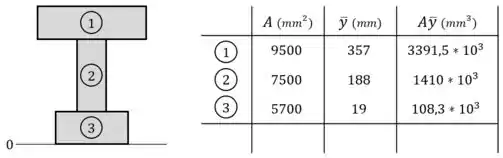
Por último, fazemos o somatório das áreas e dos produtos e colocamos esses resultados na última linha da tabela:
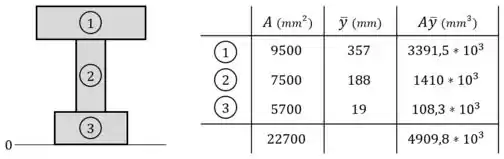
Com isso, podemos finalmente calcular a posição da linha neutra:
E com isso, do exercício já está resolvido.

Nada mal, hein?
Passo 3
Agora, vamos calcular o momento de inércia da área para essa viga.
Sabemos que o momento de inércia da área de cada retângulo ou tábua que compõe a viga vai ser dado por:
Então vamos pensar...
Para a tábua 1, nós temos uma base de e uma altura de , então:
Para a tábua 2, e , então:
E para a tábua 3, e , logo:
Em seguida, temos que cada tábua tem uma distância entre o seu centro e a linha neutra da viga:
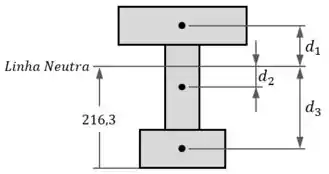
Para a tábua 1, que tem um centro com uma altura de , essa distância vai dar:
Já para a tábua 2, com seu centro com uma altura de , temos que:
E para a tábua 3, com um centro de altura de , temos:
Com isso, já definimos:
- Todos os momentos de inércia da área de cada tábua;
- Todas as distâncias de cada tábua;
- E todas as áreas de cada tábua, dispostas na tabela do passo anterior.
Então agora, só nos falta aplicar a fórmula:
E realizar esse somatório para encontrarmos o valor final de para essa viga:
Calculando tudo isso, encontramos que:
E assim, metade do exercício está resolvido!

Segura aí que tá acabando!
Passo 4
Por fim, podemos ver que, em termos absolutos, a posição em relação à linha neutra é maior para os pontos na base da nossa viga:
Do que para os pontos no topo da viga:
Ou seja, o valor máximo de (em termos absolutos) é:
E a tensão de flexão máxima na viga (em termos absolutos) é:
Daí que, substituindo:
- ;
- ;
- & ,
Temos que:
Simplificando tudo, isso fica assim:
Finalmente, calculando tudo e sabendo que é o mesmo que , encontramos que:
E olha só! Já temos a resposta do exercício!

Agora só falta o rascunho da distribuição de tensões na seção transversal.
Passo 5
Sobre essa distribuição de tensões na seção transversal da nossa viga, podemos dizer:
- Que ela varia linearmente com a variação da posição do ponto sendo estudado, como mostra a fórmula da flexão ;
- Que a posição da linha neutra em relação à ela mesmo é zero, e, portanto, na linha neutra;
- E que na base da viga, .
Se conseguirmos calcular também a tensão nos pontos do topo da viga, vamos ter informações suficientes para fazer o rascunho da distribuição de tensões.
Então vamos calcular a tensão nos pontos do topo da viga:
Substituindo:
- ;
- ;
- & ,
Encontramos que:
Com isso, considerando um eixo começando na base da viga, podemos marcar os pontos:
- para a base da viga, onde ;
- para a linha neutra, onde ;
- & para o topo da viga, onde ;
Conectando esses pontos por uma reta, conseguimos fazer o rascunho da distribuição de tensões abaixo:
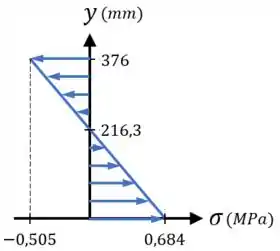
E pronto!

Terminamos o exercício.