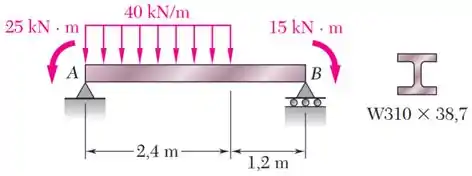
Trace os diagramas de força cortante e momento fletor para a viga e carregamento mostrados na figura, e determine a tensão normal máxima provocada pelo momento fletor.
Dados: Um perfil possui uma seção transversal simétrica na horizontal e na vertical, com altura de e momento de inércia da área .
Passo 1
O que está acontecendo?
O carregamento nessa viga vai produzir ao longo dele esforços internos na forma de forças cortantes e momentos fletores .
Daí que, em uma certa seção dessa viga, o momento fletor vai possuir o seu valor máximo em termos absolutos.
Nessa seção, ocorrerá a tensão normal de flexão máxima nessa viga, de acordo com a fórmula da flexão:
Onde:
- (ou só “”) é o momento fletor em uma seção transversal da viga;
- é a posição do ponto da seção em que se quer calcular a tensão em relação à linha neutra da seção;
- & (ou só “”) é o momento de inércia da área da seção.
Além disso...
A viga foi feita com um perfil padronizado “”, de altura e momento de inércia da área .
Esse perfil, por ser simétrico, ainda tem uma linha neutra que passa bem no meio dele:

Dessa forma, as posições em relação à linha neutra de valores críticos (máximos) nesse perfil vão ser para o topo da seção e para a base.
E o que é que o exercício quer?
Primeiro, ele quer que a gente faça os diagramas de força cortante e momento fletor para essa viga.
Para tanto, podemos recorrer aos métodos da estática: DCL, equilíbrio, análise dos esforços internos & diagramas de esforços internos.
Em seguida, ele quer que a gente determine a tensão normal de flexão máxima nessa viga.
Para tanto, podemos aplicar a fórmula da flexão utilizando os valores máximos/críticos encontrados anteriormente para e .
Passo 2
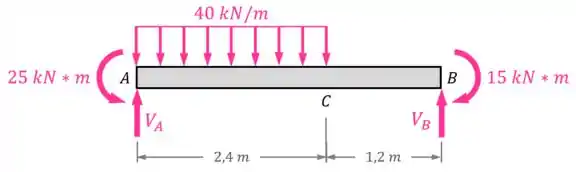
Então vamos começar com o primeiro passo dos métodos da estática, que é o DCL ou:
![]()
Para essa viga:
- O apoio fixo em vai realizar uma reação na horizontal (que vai acabar sendo nula e pode ser omitida do DCL) e uma reação na vertical .
- E o apoio móvel em vai realizar uma reação na vertical ;
Dessa forma, o nosso DCL vai ficar assim:
Passo 3
Feito o DCL, seguimos para o:
![]()
Aplicando o equilíbrio de forças na vertical, vamos ter:
Na hora de fazer esse somatório, consideramos a força distribuída uniforme de que atua ao longo do comprimento de da viga como uma força equivalente:
Dessa forma, o nosso somatório de forças na vertical fica assim:
O que significa que:
Em seguida, podemos aplicar o equilíbrio de momentos em relação ao ponto :
Aqui, como a força distribuída de é uniforme, podemos considerar que a sua força equivalente de atua bem no meio do comprimento de .
Dessa forma, temos que o braço da força equivalente de em relação ao ponto vai ser .
Sabendo disso e considerando os momentos no sentido anti-horário como positivo (), o nosso somatório de momentos fica assim:
Isolando , temos:
Calculando tudo, encontramos que:
Em seguida, substituindo isso na expressão anterior , encontramos que:
Passo 4
Encontrados os valores dos esforços externos atuantes na nossa viga, podemos seguir agora para a:
![]()
Na nossa viga, temos descontinuidades:
- em ; (início da viga, início de uma força distribuída, força concentrada e momento concentrado)
- em ; (fim de uma força distribuída)
- & em . (final da viga, força concentrada e momento concentrado)
Então precisamos avaliar as seções entre e & as seções entre e :
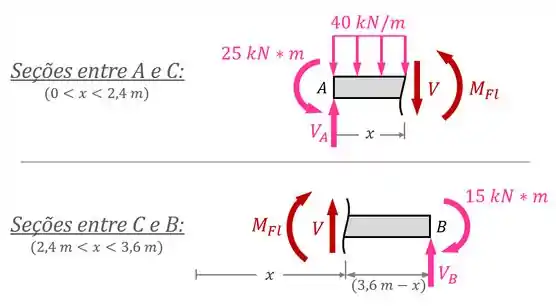
Feitos os desenhos acima, precisamos aplicar as condições de equilíbrio em cada situação para conseguirmos descrever os esforços internos e na viga.
Primeiro, analisamos as seções entre e .
Aplicando o equilíbrio de forças na vertical, temos:
Aqui, a força distribuída uniforme de que atua ao longo do comprimento pode ser considerada como uma força equivalente .
Dessa forma, o nosso somatório de forças fica assim:
Substituindo e isolando , encontramos que:
Em seguida, aplicando o equilíbrio de momentos em relação ao ponto da seção, temos:
Aqui, como a força distribuída de é uniforme, podemos considerar que a sua força equivalente de atua bem no meio do pedaço de viga que estamos estudando.
Sendo assim, o nosso somatório de momentos fica assim:
Substituindo e isolando , encontramos que:
Depois, analisamos as seções entre e :
Aplicando o equilíbrio de forças na vertical, temos que:
Isolando e substituindo , encontramos que:
Em seguida, aplicando o equilíbrio de momentos em relação ao ponto da seção, temos:
Considerando que os momentos no sentido anti-horário são positivos (), esse somatório fica assim:
Isolando e substituindo , temos que:
Fazendo a distributiva e arrumando tudo, encontramos que:
Passo 5
Por fim, podemos seguir para o último passo dos métodos da estática, que são os:
![]()
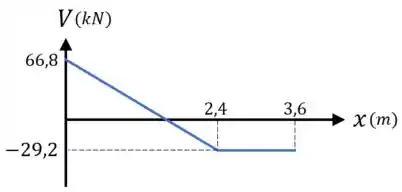
Para a força cortante , temos:
- Que ela segue a equação quando , variando linearmente entre os pontos e ;
- E que ele é igual quando .
Dessa forma, o diagrama da força cortante fica assim:
Quanto ao momento fletor , ele é descrito por duas equações:
Primeiro, para , ele é descrito pela função quadrática:
O que significa que ele varia parabolicamente, com uma concavidade para baixo (uma vez que a segunda derivada dessa função acima é negativa), entre os pontos:
Além disso...
Fazendo a primeira derivada dessa função e igualando-a a zero, encontramos que o ponto crítico dessa função é .
E, como a função tem uma concavidade para baixo, esse ponto crítico vai ser o seu ponto de máximo.
Calculando o valor de para esse ponto, temos:
Em seguida, para o trecho , temos uma função de primeiro grau:
Dessa forma, temos que nesse trecho, o momento fletor varia linearmente entre os pontos:
Tendo tudo o que vimos em mente, conseguimos desenhar o diagrama de momento fletor para essa viga, que fica assim:
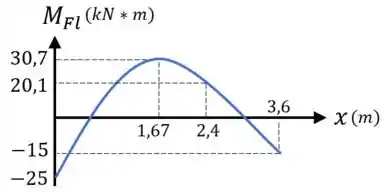
Aí, desse diagrama acima, conseguimos identificar que o momento fletor máximos em termos absolutos nessa viga é:
E assim terminamos toda a parte dos métodos da estática!
Passo 6
Agora, como o exercício já nos forneceu as propriedades geométricas da seção transversal dessa viga, podemos seguir direto para o cálculo da tensão normal de flexão máxima na viga.
Para tanto, podemos aplicar a fórmula da flexão:
Substituindo nessa fórmula:
- O momento fletor máximo na viga ;
- Os valores críticos de , ;
- E o valor de , ,
Vamos encontrar as tensões máximas de tração e de compressão na nossa viga:
Simplificando, isso fica assim:
Calculando tudo e sabendo que é o mesmo que , encontramos que as tensões máximas de tração e compressão nessa viga são:
Sendo que o valor negativo, de compressão, ocorre no topo da viga, onde , e o valor positivo, de tração, ocorre na base da viga, onde .
Finalmente, na hora de darmos o resultado final do exercício, podemos indicar só o valor absoluto desse resultado: