Uma viga engastada em uma de suas extremidades sofre o carregamento mostrado abaixo. Sabendo que essa viga suportará uma carga triangular distribuída, determine o máximo valor que essa carga distribuída terá para que não haja rompimento da peça.
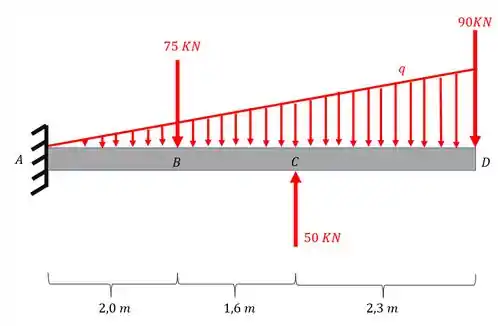
Passo 1
Como se trata de uma questão em que só consideraremos a contribuição dos esforços normais, e também temos uma resistência a tensão Normal, sabemos que a fórmula que devemos usar é a fórmula da flexão que é dada por
Mas podemos considerar algumas suposições, por exemplo, como queremos definir um valor máximo de carga, podemos fazer esse cálculo pelo módulo, ou seja, podemos retirar o sinal da nossa fórmula
Outra coisa que sabemos é que devemos usar a igualdade
Pois assim conseguiremos determinar o valor máximo que a peça aguenta sem romper.
Por fim, uma coisa que também temos que fazer é determinar o momento máximo que ocorre na nossa peça em função da nossa carga. Devemos usar o momento máximo pois queremos o ponto em que a viga será mais solicitada. Se ela suportar os esforços nesse ponto, aguentará em qualquer ponto.
Passo 2
Como a nossa viga está engastada, e todos os carregamentos maiores estão na mesma direção, o maior momento que a nossa viga estará sujeita ocorrerá na parede, ou seja, no ponto A.
Para determinarmos o valor desse momento devemos desenhar o nosso diagrama de corpo livre
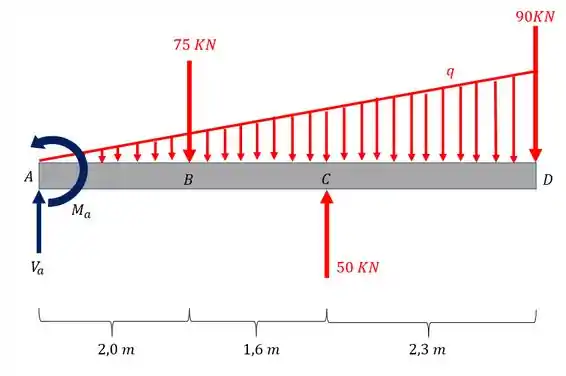
Com o nosso diagrama de corpo livre devemos fazer o equilíbrio da nossa peça para podermos calcular as reações de apoio
Podemos então isolar o valor de , e dessa forma teremos que
Agora que já determinamos o valor da reação vertical, vamos calcular o momento em A
E esse momento que calculamos é o nosso momento máximo
Passo 3
Agora que já temos o valor do nosso momento, precisamos definir os outros dois valores da nossa fórmula, que são os valores do momento de inercia e do y.
Vamos primeiro definir o nosso momento de inércia. Como a nossa seção é quadrada, sabemos que o momento de inércia é dado por
Como é uma seção quadrada, sabemos que
Substituindo na nossa fórmula teremos que
Como já dissemos antes também precisamos do valor de y, com isso teremos que
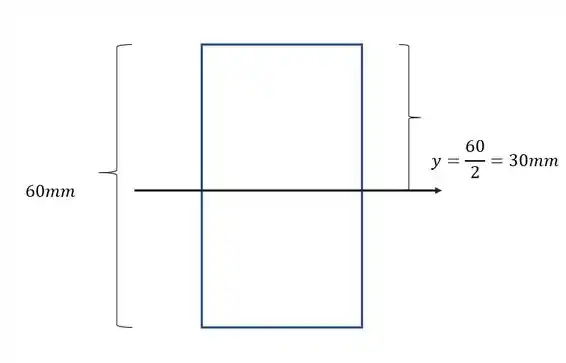
Como queremos sempre o valor máximo, sempre usaremos o valor mais distante da linha neutra. Como a nossa peça tem seção quadrada, a linha neutra passa exatamente no centro dela. Dessa maneira teremos que
Passo 4
Agora já temos a nossa fórmula
E os nossos valores
Basta que substituamos eles na nossa fórmula
Deixando o parêntese isolado teremos que
Isolando o valor de P