Uma bolha de ar de está no fundo de um lago a profundidade, onde a temperatura é . Ela se solta e vai para a superfície, onde a temperatura é de. Considere a temperatura da bolha como sendo a mesma da água à sua volta e encontre o seu volume exato no momento antes em que alcança a superfície – ainda na água.
Passo 1
Vamos que vamooos !!
Vamos desenhar o que está acontecendo para ficar mais claro:
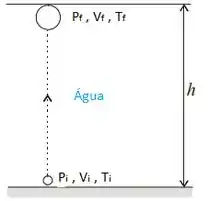
Vamos guardar esta informação no coração, ok?
Bom galerinha, se o gás é ideal vocês já sabem qual equação usar, não é?
Onde é a pressão, o volume, o número de mols, a temperatura e a constante dos gases ideais ou constante de Clapeyron.
Bom, como a quantidade de ar dentro da bolha não varia, é constante assim como a contante dos gases ideais!
Então, como o termo não varia nestas situações, vamos passar a temperatura para o outro lado da igualdade dividindo:
Se este termo é igual para as duas situações podemos escrever:
Achamos a equação que precisamos, mas queremos o volume final , certo? Então temos que dar um jeito do ficar sozinho.
Primeiro vamos passar para o outro lado da igualdade multiplicando:
E a pressão final () vai para o outro lado, mas dividindo:
Shoow de bolinhas!! Já achamos a equação, agora só precisamos dos valores para cada um dos termos.
Passo 2
Para a situação inicial temos:
Bom, a temperatura deve ser dada em e o volume em m³ !! Vamos lembrar das transformações?
Então:
E para o volume temos que tomar cuidado. Para passar de para metros precisamos multiplicar por :
Mas precisamos passar para , então basta elevar os dois lados ao cubo
Quando elevamos uma potência a algum expoente, temos que multiplicar os expoente
Então:
E a pressão? Bom, a pressão vai ser devido a pressão atmosférica mais a pressão da coluna de água, não é?
Vamos colocar matematicamente:
Algumas inforações não foram dadas no enunciado, é imporante que saiba de cabeça
Lembrando que:
Substituindo:
Passo 3
Achamos tudo que queríamos para a situação inicial, agora só nos resta achar os dados para a posição final!!
E a pressão final, como a bolha está na superfície, é somente a pressão atmosférica:
E agora é só substituir:
Para transformar em para ficar mais legal, vamos usar a relação do Passo e fazer uma regrinha de três bem simples:
Multiplicando cruzado:
Para isolar o , o termo passa para o outro lado da igualdade dividindo:
Repare que as unidade em cima e em baixo podem ser cortadas, restando apenas
Essa foi massa demais, não foi?!