Considere dois números reais positivos tais que

Queremos minimizar a quantidade . Para isso:

1. Determine uma função de uma variável tal que o valor mínimo de corresponda à solução do problema acima. Indique também o domínio dessa função.
2. Determine o valor mínimo de , justificando sua resposta.

Considere a função dada por:

1. Determine, caso exista(m):

(a.1) O(s) intervalo(s) de crescimento e decrescimento de .

(a.2) O(s) ponto(s) de máximo local e de mínimo local de .

(a.3) O(s) intervalo(s) onde o gráfico de tem concavidade voltada para cima e onde tem concavidade voltada para baixo.

(a.4) O(s) ponto(s) de inflexão do gráfico de .

b) Faça um esboço do gráfico de indicando explicitamente o(s) ponto(s) de máximo, de mínimo e de inflexão determinado(s) nos itens anteriores. Esboce também a(s) reta(s) tangente(s) ao gráfico de no(s) ponto(s) em que a derivada é zero e no(s) ponto(s) de inflexão.

Passo 1

(a.1) Para saber os intervalos de crescimento e decrescimento temos que analisar o sinal da derivada de . Então vamos começar derivando a função:

f ' ( x ) depende apenas de , pois é sempre positivo. Como é uma parábola de concavidade pra cima que corta eixo em e, ocorre o seguinte:

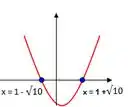
Assim:

Intervalo de crescimento de :

Intervalo de decrescimento de :

Passo 2

(a.2) Vamos achar os pontos críticos para podermos determinar os máximos e mínimos locais, se existirem.

A próxima etapa é fazer o Teste da Primeira ou da Segunda derivada. Nesse caso, já que temos o gráfico do item anterior pra ajudar, vamos fazer o Teste da Primeira Derivada, ou seja, analisar o sinal da derivada perto dos pontos críticos. Olha só:

• Em a derivada muda de positiva para negativa, logo esse é um ponto de máximo local
• Em o sinal da derivada não muda, logo não é nem máximo nem mínimo local
• Em a derivada muda de negativa para positiva, logo esse é um ponto de mínimo local

R delimitada por uma reta e uma parábola, conforme o esboço abaixo:

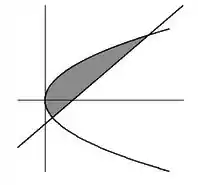
Sabendo que:

• A parábola possui vértice na origem e passa pelo ponto
• A reta passa pelos pontos e

1. Determine a equação da parábola e a equação da reta
2. Descreva a região através de um conjunto de desigualdades
3. Escreva a área da região através de uma integral ou de uma soma de integrais (Não é necessário calcular a integral)
4. Calcule a área da região