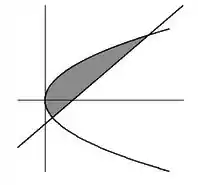
Sabendo que:
- A parábola possui vértice na origem e passa pelo ponto
- A reta passa pelos pontos e
- Determine a equação da parábola e a equação da reta
- Descreva a região através de um conjunto de desigualdades
- Escreva a área da região através de uma integral ou de uma soma de integrais (Não é necessário calcular a integral)
- Calcule a área da região
Passo 1
- Observando a figura, vemos que a parábola é do tipo deitada e com vértice na origem, logo sua equação é do tipo . Como ela passa pelo ponto podemos substitui-lo nessa equação e encontrar o coeficiente :
- Vamos tentar entender o que é essa região dada, que está compreendida entre os gráficos da parábola e da reta.
- Como o item pede pra gente determinar uma integral que represente a área da região , sabemos que essa integral precisa der definida. Então, primeiro temos que achar as interseções entre as curvas pra podermos saber o intervalo de integração que vamos usar na integral. Pra isso, podemos substituir a equação da parábola na da reta:
- Pra calcular a área de temos que resolver a integral definida que acabamos de determinar. Vamos primeiro integrar indefinidamente a função, assim:
Agora temos a equação dessa parábola, que é:
Passo 2
Agora falta achar a equação da reta, que genericamente é
Se substituirmos os dois pontos dados por onde a reta passa, vamos conseguir descobrir os coeficientes e .
Opa! Descobrimos o coeficiente linear da reta. Agora vamos substituir o outro ponto:
Portanto a equação da reta é
Passo 3
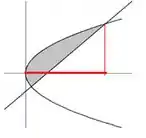
Matematicamente, a gente pode escrever isso dessa forma:
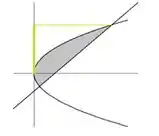
Escrevendo essa conclusão em “matematiquês” vamos ter:
Portanto, a região pode ser descrita pelas desigualdades:
Passo 4
Substituindo os valores de encontrados na equação da reta vamos obter os valores de , e os pontos de interseção vão ser:
E
Passo 5
Olhando em relação ao eixo , a área de corresponde a área abaixo da reta menos a área abaixo da parábola, então dentro da nossa integral ficaria uma coisa assim:
Como não podemos integrar em relação a duas variáveis, vamos reescrever a equação da reta de modo a tirar a variável (já que estamos olhando em relação ao eixo a integral será em relação à ).
Voltando pra subtração que fizemos ali em cima, o que teríamos então dentro da integral seria:
Passo 6
Só falta a gente definir qual vai ser o intervalo de integração. Perceba que o varia de um ponto de interseção ao outro, então vamos integrar de
até
Passo 7
Agora é só montar a integral!
Passo 8
Voltando pra integral definida, ficamos com:
Resolvendo:
Pronto! A área de equivale a
Resposta
a) e
b)
c)
d)