UNB-Calculo 1 – Listas de aplicação em cálculo 1 - Lista 10 – 2020.2
Suponha que, no instante , a posição em relação à origem de uma partícula que se desloca ao longo de uma reta seja dada por em que é a função velocidade, cujo gráfico está ilustrado abaixo. Considere ainda que seja dado em segundos, que seja dada em metros e que, para , o gráfico de seja um segmento de reta. A partir do gráfico da função velocidade, julgue os itens a seguir.
- A partícula está se afastando da origem entre os instantes .
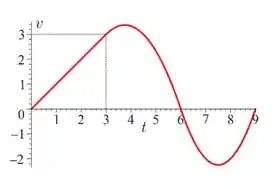
- A partícula percorre menos de metros nos primeiros segundos.
- No instante a partícula está na origem.
- No instante a posição da partícula é positiva.
- O espaço total percorrido pela partícula igual a
Passo 1
E ae galerinha do responde Aí, meu nome é Rodolpho e hoje vamos resolver mais uma questão de Cálculo aplicado.
Para resolver essa questão precisamos de alguns conceitos, por sorte, todos os conceitos estão descritos na questão.
Por sorte, vamos utilizar apenas conceitos de integral aqui. É isso aí, são as famosas integrais.
Calminha, Calminha. Vamos resolver juntinhos e vou te mostrar que não são conceitos tão complicados.
De uma forma prática, precisamos falar quais alternativas são verdadeiras utilizando os conceitos informados na questão.
E ae, bora começar a responder?
Passo 2
Para responder a primeira alternativa, precisamos da seguinte expressão fornecida pela questão:
No intervalo temos que , sendo assim temos que:
Portanto, o espaço está aumentando. Confirmando que a primeira alternativa está verdadeira.
Passo 3
Para resolver a segunda alternativa, precisamos novamente da seguinte informação da questão:
Como a função começa do 0, temos que:
Quando . Calculando que
Sendo assim, temos que:
Como temos que , confirmando que a segunda alternativa é falsa.
Passo 4
Para responder a alternativa , apenas precisamos analisar o gráfico. A velocidade é nula no instante . Porém, não podemos afirmar que ele retornou para a posição inicial. Logo é falsa.
Passo 5
Para responder a alternativa d) precisamos saber o conceito de área, que é o seguinte:
Logo, a área abaixo da função no intervalo é calculado através da integral. Portanto:
No intervalo podemos verificar nos gráficos que a velocidade é negativa, sendo assim:
Analisando o gráfico temos que portanto:
Logo, a alternativa d) é verdadeira.
Passo 6
Para responder a alternativa precisamos calcular o espaço total, para isso vamos precisar da seguinte informação da questão:
Utilizando as propriedades de integral é melhor quebrarmos o limite de integração da seguinte forma:
Como a velocidade no intervalo [6,9] é negativa. O espaço total se torna:
Mostrando que a última alternativa é verdadeira.
Resposta
Ei, a resposta está no passo a passo :)