UNB-Calculo 1 – Listas de aplicação em cálculo 1 - Lista 10 – 2020.2
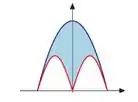
A figura ao lado indica a área delimitada pelos gráficos das funções
E
Com . Use a integral definida para calcular o valor dessa área.
Passo 1
Opa irmãozinho do Responde Aí, tá tudo de boas?
Aqui temos uma questãozinha para calcular a área de uma certa figura utilizando o conceito de integrais definidas.
Mas e aí, tu lembra que conceito é esse?
Não lembra? Oxe, relaxa. Precisamos apenas lembrar desse conceito aqui:
E com isso, vamos resolver tudo.
Mas Calminha, Calminha. Vamos resolver juntinhos e vou te mostrar que não são conceitos complicados.
E ae, bora começar a responder?
Passo 2
Para resolver essa questão precisamos da seguinte informação:
Agora precisamos descobrir quem é a. Vamos analisar a figurinha. Belezinha?
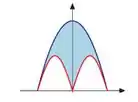
Analisando a figurinha vemos que a área é delimitada superiormente pela função quadrática, e inferiormente pela função seno, logo
Portanto:
Agora precisamos resolver a função modular, utilizando a propriedade do modulo temos que:
Portanto precisamos utilizar a seguinte propriedade da integral:
Aplicando as propriedades da função modular temos que:
Passo 3
Agora vamos resolver a integral:
Aplicando a linearidade das integrais temos que:
Aplicando os limites de integração temos que:
Resposta
Ei, a resposta está no passo a passo :)