Provas Profº Rómulo Castillo de Cálculo 2 da UFSC - P2 2014.2
Cálculo 2 - UFSC
Questão 1. Calcule cada uma das seguintes integrais e determine se for convergente ou não conforme corresponda:
c)
Ver solução completaQuestão 2. Dados os gráficos de , e as regiões , , , e , delimitadas seguem a figura anexa, formule, em cada caso, a integral que calcula o volume do sólido obtido ao girar a região indicada ao redor do eixo apontado.
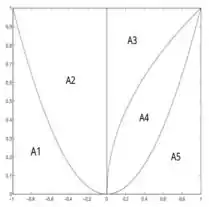
a) ao redor da reta .
Ver solução completaQuestão 2. Dados os gráficos de , e as regiões , , , e , delimitadas seguem a figura anexa, formule, em cada caso, a integral que calcula o volume do sólido obtido ao girar a região indicada ao redor do eixo apontado.
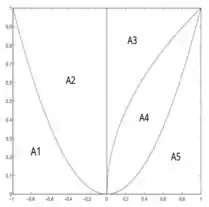
b) ao redor de .
Ver solução completaQuestão 2. Dados os gráficos de , e as regiões , , , e , delimitadas seguem a figura anexa, formule, em cada caso, a integral que calcula o volume do sólido obtido ao girar a região indicada ao redor do eixo apontado.
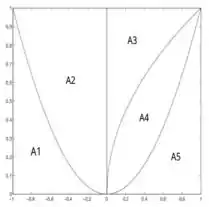
c) ao redor de .
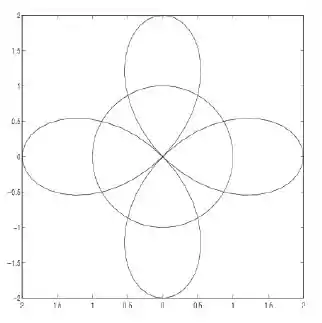
Ver solução completaQuestão 3. Sejam as curvas e desenhadas em anexo. Formule, em cada caso, uma integral para calcular:

a) A área da região interior a ambas as curvas
Ver solução completaQuestão 3. Sejam as curvas e desenhadas em anexo. Formule, em cada caso, uma integral para calcular:
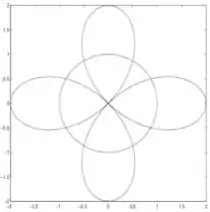
b) A área fora do círculo e interior à rosa.
Ver solução completaQuestão 3. Sejam as curvas e desenhadas em anexo. Formule, em cada caso, uma integral para calcular:
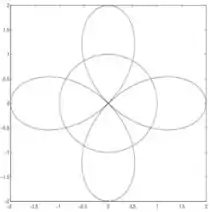
c) A área exterior à cardioide e interior ao círculo.
Ver solução completa1) Calcule cada uma das seguintes integrais e determine se for convergente ou não conforme corresponda:
a)
Ver solução completa