UFSC, Joinville, Cálculo II, Provas Profº Rómulo Castillo - P2 2014.2, Questão 2b
Questão 2. Dados os gráficos de , e as regiões , , , e , delimitadas seguem a figura anexa, formule, em cada caso, a integral que calcula o volume do sólido obtido ao girar a região indicada ao redor do eixo apontado.
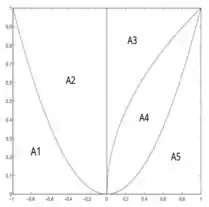
b) ao redor de .
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nesse problema temos que obter o volume do solido de revolução cuja área que vamos revolucionar é dada por e o eixo de revolução é em .
Como vamos resolver esse problema? 😐😐
Podemos usar o método dos discos, ou seja, usar a fórmula do volume de um disco para resolver o problema.
O volume do disco, é dado por , onde é o raio e a altura.
Se dividirmos o volume em discos de alturas infinitesimais, podemos chamar de e de .
Dessa forma, o volume do solido é dado por
Bora lá! 😁
Passo 2
Analisando a região , temos que como a rotação acontece em , podemos adaptar a função para facilitar nossos cálculos.
A função que vai determinar é e
Queremos uma função , então isolamos na igualdade
No caso, o raio varia de até , ou seja, temos que substituir por onde e resultando em uma integral volumétrica
Por fim, temos que definir os limites de integração e .
Pelo que vemos na imagem da região, a altura em da região varia de a , portanto, temos que integrar entre e .
Substituindo os limites de integração, e a função , temos
Tranquilo até aqui? 😎
Passo 3
Resolvendo a integral, temos...
Integrando pelo método de integração polinomial...
Aplicando o limite de integração...
É isso! Essa resolução te ajudou? Responde Aí! ✌
