UFSC, Joinville, Cálculo II, Provas Profº Rómulo Castillo - P2 2014.2, Questão 3a
Questão 3. Sejam as curvas e desenhadas em anexo. Formule, em cada caso, uma integral para calcular:
a) A área da região interior a ambas as curvas
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nessa questão, queremos obter uma integral que resulte na área entre as curvas e escritas em coordenadas polares.
Como podemos fazer isso? 🤔
Para calcularmos uma área através de uma integral, definimos nossa região de integração e aplicamos nos limites de integração da integral de , ou seja
Onde é a região de integração.
Bora ver como fica no nosso caso? 🤔
Passo 2
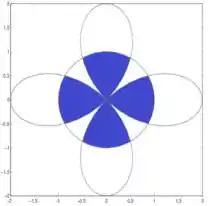
Foi pedido a área dentro da circunferência de raio e dentro da cardioide , ou seja, a região hachurada em roxo.
Em coordenadas polares, calculamos uma área por uma integral dupla em que descreve a variação do raio da região em relação à origem e o ângulo que a região faz com a origem do sistema.
Analisando a região, vemos que o raio maior está em e o raio inferior é definido pela cardioide , logo, podemos definir que .
Já em , vemos que a região dá uma volta completa ao redor da origem do sistema, ou seja, .
Com essas informações, podemos montar a integral dupla em coordenadas polares, como
Fim! Iae, o que achou? Responde Aí! 😁
