Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Comprimento de Arco

Ver Teoria
Exercício 1612345678910111213141517181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768

Enunciado

UFSC – Cálculo 2 – Prof. Dr. Romulo Castillo – P2 – 2014/2

3) Sejam as curvas r 1 = 2 cos ⁡ 2 θ e r 2 = 1 Desenhadas em anexo. Formule, em cada caso, uma integral para calcular:

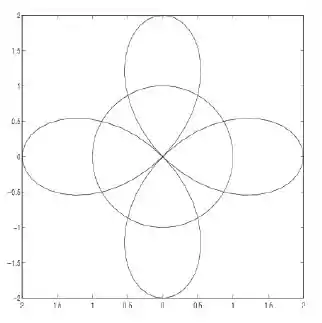
d) O comprimento de arco da rosa de 4 pétalas

Passo 1

Falaaa... tudo bem??

Nessa questão vamos o comprimento de arco da rosa do desenho.

Como temos equações em coordenadas polares, usaremos a fórmula do comprimento do arco para coordenadas polares:

L = ∫ a b r θ 2 + d r d θ 2 d θ

Passo 2

Antes de sair aplicando a fórmula, vamos achar quais são os valores de θ de onde as duas curvas se cruzam:

r 1 = r 2

2 cos ⁡ 2 θ = 1

cos ⁡ 2 θ = 1 2

2 θ = π 3

θ = π 6

Passo 3

Vamos fazer um desenho desses ângulos pra enxergar melhor:

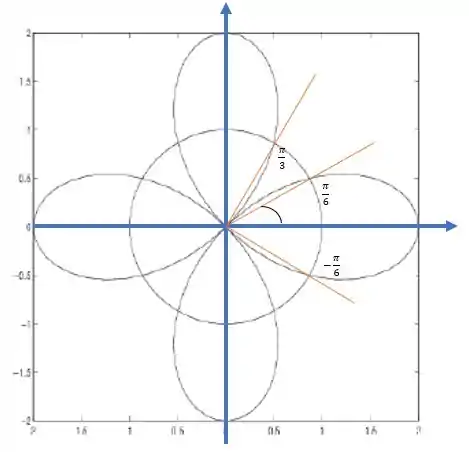
Para a pétala, que a equação é r 1 = 2 cos ⁡ 2 θ , então o comprimento de cada pétala (repara que o ângulo varia de - π 6 até π 6 ) :

L 1 = ∫ - π 6 π 6 r 1 θ 2 + d r 1 d θ 2 d θ

Para o miolo, que a equação é r 2 = 1 , então o comprimento de cada partezinha entre as pétalas (repara que o ângulo varia de π 6 até π 3 ):

L 2 = ∫ π 6 π 3 r 2 θ 2 + d r 2 d θ 2 d θ

Maaaas temos 4 pétalas e 4 partes entre as pétalas, né? Então falta somar tudo:

L t o t = 4 L 1 + L 2

= 4 ∫ - π 6 π 6 r 1 θ 2 + d r 1 d θ 2 d θ + ∫ - π 6 π 6 r 1 θ 2 + d r 1 d θ 2 d θ

Resposta

4 ∫ - π 6 π 6 r 1 θ 2 + d r 1 d θ 2 d θ + ∫ - π 6 π 6 r 1 θ 2 + d r 1 d θ 2 d θ

Exercícios de Livros Relacionados

(a) Trace a epitrocoide com equações x = 11 cos ⁡ t - 4 cos ⁡ 11 t 2 y = 11 sen ⁡ t - 4 sen ⁡ 11 t 2 Qual intervalo do parâmetro fornece a curva completa?b) Use seu SCA para calcular o comprimento apr
Um barbante é enrolado ao redor de um círculo e então desenrolado, sendo mantido esticado. A curva traçada pelo ponto P no final do barbante é chamada involuta do círculo. Se o círculo tiver raio r e
Calcule o comprimento exato da curva polar: r = 2 c o s θ 0 ≤ θ ≤ π
51-54. Use uma calculadora ou um computador para encontrar o comprimento do laço, com precisão de quatro casas decimais. Se necessário, use um gráfico para determinar o intervalo de parâmetro.53. r =
Ao gravar apresentações ao vivo, os engenheiros de som usam um padrão de captação em forma de cardioide, pois ele suprime o barulho da audiência. Suponha que o microfone esteja colocado a 4m da frente