03) Considere um circuito RC onde a força eletromotriz é uma constante , a capacitância é dada por e a resistência é dada por . Temos que as quedas de tensão no capacitor e na resistência são dadas, respectivamente, por e , onde é a carga no capacitor. A segunda lei de Kirchoff diz que a soma das quedas de tensão num circuito é igual à força eletromotriz.
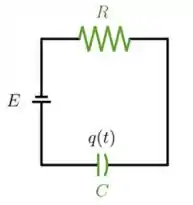
a) Mostre que a carga satisfaz uma equação da forma .
b) Encontre uma primitiva de e determine e também .
c) Obtenha a solução geral da equação determinada no primeiro item.
d) Determine a solução com carga inicial . Mostre que mostrando que esse limite não depende da carga inicial .
Passo 1
Oii gente, tudo bem?
a) Nessa questão temos um problema de física elétrica com aplicação bem interessante das nossas queridas EDO’s. Basicamente, temos um resistor com resistência variável seguindo:
Um capacitor também com capacitância variável:
E uma força eletromotriz constante valendo .
O objetivo inicial é mostrarmos que satisfaz a EDO:
Então vamos lá! O enunciado nos fala que, pela segunda lei de Kirchoff, a soma das quedas de tensão ao longo do circuito é igual à força eletromotriz. Daí, sendo e as quedas de tensão no capacitor e resistor, respectivamente, podemos escrever que:
Substituindo os dados do enunciado, chegamos a:
Pra encontrar o formato que estamos procurando, vamos dividir tudo por . Assim:
Excelente! Sendo e , podemos reescrever a equação como:
O que é exatamente o que queríamos mostrar 😊
Passo 2
b) Nesse item devemos encontrar a primitiva, , de e calcular e . Lembrando que a primitiva é simplesmente a integral da função, tipo:
Daí, como , temos:
Aqui a gente tem que ter o pulo do gato!

Chamando , temos . Ou seja:
Logo, como a resistência é sempre positiva, vale:
Massa! Bora calcular as exponenciais agora:
Muito bom! Menos um itemmmm, falta pouco!
Passo 3
c) Aqui precisamos calcular a solução geral da EDO encontrada no item a:
Mas essa é uma EDO linear de ordem, certo? Vocês lembram da solução geral?

Hahaha! Bora revisar então. Se temos uma EDO linear de ordem do tipo:
A solução geral é dada por:
Excelente! Já calculamos boa parte desses termos no item b, substituindo temos:
Logo, a solução geral é dada por:
Aeee, conseguimos. Falta só o último item agora! Simbora pessoal.
Passo 4
d) Pra finalizar a questão, primeiro devemos calcular a solução particular para o caso .
É só substituirmos na nossa solução geral para determinar o valor da constante. Daí:
Substituindo de volta na solução geral, iremos determinar a solução particular pedida. Então:

Agora é só calcularmos o .
Pensa comigo, a função do numerador é limitada pois a seno é limitada. Já no denominador, o termo faz todo denominador tender a infinito junto com . Logo, estamos calculando um limite do tipo . Portanto, podemos afirmar que:
Colocar no final de demonstração é muito chique galera, fica a dica aí haha!
Mas é isso, obrigado pela atenção de vocês! Tamo junto 😊
Resposta
a) Resolução no texto.
b)
c)
d)