02) Considere um circuito RC onde a força eletromotriz é alternada, de modo que , a capacitância é uma constante e a resistência aumenta linearmente, de modo que . Temos que as quedas de tensão no capacitor e na resistência são dadas, respectivamente, por e , onde é a carga no capacitor. A segunda Lei de Kirchoff diz que a soma das quedas de tensão num circuito é igual à força eletromotriz.
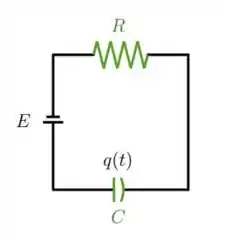
a) Mostre que a carga satisfaz uma equação da forma .
Para os próximos itens considere que .
b) Encontre uma primitiva de e determine e também .
c) Obtenha a solução geral da equação determinada no primeiro item.
d) Determine a solução com carga inicial . Mostre que , mostrando que esse limite não depende da carga inicial .
Passo 1
Eaí gente, tudo bem?
a) Nessa questão temos um circuito RC no qual a resistência varia em função do tempo seguindo:
E que a força eletromotriz é alternada, obedecendo:
Precisamos mostrar que a carga no capacitor, , obedece à equação:
Beleza! Mas como podemos fazer isso?

Hahaha calma, não precisa ter muito conhecimento de física. O próprio enunciado já nos diz o que fazer! Pela Lei de Kichorff, a soma das quedas de tensão no circuito é igual à força eletromotriz.
Daí, sendo e as quedas de tensão no capacitor e resistor, respectivamente, podemos escrever que:
Substituindo o valor de , temos:
Como queremos deixar no formato bonitinho de EDO linear de ordem, vamo dividir tudo por :
Perfeito gente! Se chamarmos e , temos:
O que é exatamente o que queríamos encontrar 😉
Passo 2
b) Beleza! A partir de agora ganhamos alguns valores iniciais pra questão não ficar tão literalzona!

Temos .
Aqui precisamos encontrar a primitiva da função . Vocês lembram o que é uma função primitiva?
Basicamente é o resultado da integral, tipo:
Sacaram?! Além disso devemos calcular também e . Então bora lá!
Como pelo item a, achamos que:
Temos:
Logo:
Fazendo , então .
Muito bom! Calculando as exponenciais, ficamos com:
Passo 3
c) Ok! Aqui precisamos determinar a solução geral da EDO que encontramos no item a:
Substituindo os dados atuais, a gente pode reescrever essa equação como:
Massa! Relembrando que essa é uma EDO linear de 1° ordem.
“Linear” porque todas as variáveis e ) estão elevadas a , e é de ordem porque a variável de maior grau de derivação é .
Vocês lembram a solução geral desse tipo de equação?!
Legal que no item b calculamos boa parte desses parâmetros, por isso já sabemos que:
Agora é só substituir na solução geral:
Logo:
Prontinho 😊
Passo 4
d) Pra encerrar mais uma questão, devemos determinar a solução particular para o caso e depois calcular .
Começando pela solução particular, se , temos:
Logo:
Substituindo de volta na solução, encontraremos a solução particular:
Fazendo o limite quando tende ao infinito, vem:
Aí pensa comigo, a função que tá no numerador é limitada. Já no denominador, quando , também. Logo, esse limite é do tipo , por isso vale zero.
O que mostra que, de fato, a carga final não depende de .
Prontinho galera! Mais uma questão resolvida, se precisar de um help tamo aqui 😊
Resposta
a) Resolução no texto.
b)
c)
d)