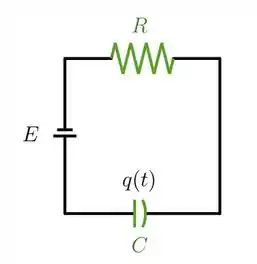
01) Considere um circuito onde a força eletromotriz é uma constante , a capacitância é uma constante e a resistência aumenta linearmente, de modo que . Temos que as quedas de tensão no capacitor e na resistência são dadas, respectivamente, por e , onde é a carga no capacitor. A segunda Lei de Kirchoff diz que a soma das quedas de tensão em um circuito é igual à força eletromotriz.
a) Mostre que a carga satisfaz uma equação da forma . Mostre também que a carga constante é uma solução, conhecida como carga estacionária.
Para os próximos itens considere .
b) Encontre uma primitiva de e determine e também .
c) Obtenha a solução geral da equação determinada no primeiro item.
d) Determine a solução com carga inicial . Mostre que, para qualquer carga inicial, após muito tempo decorrido a carga se aproxima da carga estacionária, isto é, mostre que .
Passo 1
Faaaala galera!! Tudo certo com vocês?
a) Calma, vocês não estão na página errada, essa questão é de cálculo mesmo hahaha!
Aqui temos um probleminha de circuito RC, mas não precisamos de conhecimento físico para resolvê-lo.
Nesse primeiro item precisamos mostrar que obedece a uma EDO do tipo:
Ou seja, uma EDO linear de ordem.
Para isso, o enunciado nos fala que pela segunda lei de Kirchoff, a soma das quedas de tensão em um circuito é igual à força eletromotriz.
Como e são as quedas de tensão no capacitor e no resistor, respectivamente; e é a força eletromotriz do circuito, podemos escrever que:
Como a resistência varia com o tempo segundo a , podemos reescrever a equação. Daí:
Agora é só a gente ajeitar os detalhes pra deixar no formato pedido da questão. Dividindo os dois lados por , vem:
Prontinho, sendo e , conseguimos mostrar que obedece à EDO do tipo
Além disso, também precisamos mostrar que , constante com o passar do tempo, é solução da EDO. Para isso, basta mostrar que a EDO acima é obedecida quando fazemos .
Já que é constante nesse caso, . Substituindo essas informações temos:
Massa! Mostramos que essa solução obedece a equação do problema 😉
Passo 2
b) Agora temos alguns valores dados: .
A questão nos pede para determinar uma primitiva de e depois calcular . Ou seja, inicialmente temos que calcular:
Lembra que, pelo item anterior, temos:
Substituindo os novos dados desse item, ficamos com:
Logo:
Como só queremos uma primitiva, vamos considerar .
Daí, só pra deixar mais bonitinho e facilitar a próxima parte, vamos fazer:
Agora, podemos calcular . Assim:
Excelente! Lá se foi mais um item 😊
Passo 3
c) Aqui devemos calcular a solução geral da EDO:
Considerando , temos:
Temos uma EDO linear de ordem não-homogênea. Vocês lembram como podemos resolvê-la?

O bizu galera é lembrar que em equações do tipo:
A solução geral é dada por:
Pra achar isso é só aquela técnica do fator integrante, tão ligados?
Mas beleza, bora calcular os termos da solução geral. Pelo item anterior, sabemos que:
Massa! Agora vamo calcular essa integral.
Usando a mudança de variável, podemos fazer:
Logo:
Substituindo de volta, chegamos que:
Juntando tudo na solução geral, temos:
Pra finalizar, a solução geral é da forma:
Passo 4
Nesse último item precisamos calcular a solução particular quando , e mostrar .
Vamos por partes! No item anterior encontramos a solução geral da forma:
Usando , vem que:
Logo, o que a questão tá pedindo pra gente é justamente:
Top! Pra terminar de matar de vez essa questão é só calcular:
O negócio é perceber que quando , no segundo termo do nosso limite, algo limitado no numerador dividido por um número gigante no denominador. Isso dá zero! Por isso:
Que é exatamente o que estávamos querendo mostrar 😊

Então é isso, espero que vocês tenham entendido bem direitinho.
Até a próxima, tamo junto!
Resposta
a) Resolução no texto.
b)
c)
d)