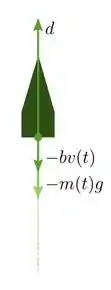
04) Num foguete, se o empuxo é uma constante , a taxa de variação de sua massa é constante, de modo que . Se o foguete não atinge uma altura muito elevada, podemos supor que a gravidade é uma constante e que a força de arraste do ar é dada por , proporcional à velocidade do foguete. Segue que a força que atua no foguete é dada por:
Neste caso, a segunda lei de Newton é dada por:
a) Mostre que satisfaz uma equação da forma .
Para os próximos itens considere .
b) Encontre uma primitiva de e determine e também .
c) Obtenha a solução geral da equação determinada no primeiro item.
d) Determine a solução com velocidade inicial . Para que valores de a velocidade está definida?
Passo 1
Faaaaala galerinha, todo mundo animado pra matar mais uma questão?
a) Esse exercício traz um contexto física interessante envolvendo a força de resistência do ar para treinarmos as EDO’s. Basicamente, precisamos mostrar que se encaixa na EDO do tipo:
Massa! Pra conseguir chegar nisso recebemos duas equações:
Assim, aplicando a regra da cadeia na segunda equação, temos:
Como . Substituindo nas nossas duas equações, vem:
Igualando as duas, temos:
Pra ficar no formato que a gente quer, bora dividir os dois lados por . Vem:
Olha que massa! Agora, chamando e , e reescrevendo a equação em , ficamos com:
O que é exatamente o queríamos mostrar! 😊
Passo 2
b) Aqui temos alguns dados numéricos importantes:
devemos determinar uma primitiva de e calcular as exponenciais , .
Mas vocês lembram como calcular a primitiva de uma função?
A primitiva de uma função nada mais é que a sua integral. Assim:
Substituindo a função que achamos no item a, temos:
Fazendo , vem Assim:
Lembrando que a massa é sempre positiva, vem:
Substituindo os dados numéricos:
Logo:
Top! A primeira parte já foi. Calculando agora as exponenciais, temos:
Passo 3
c) Nesse item precisamos calcular a solução geral da EDO desenvolvida no item a.
Substituindo os dados numéricos:
Essa equação é uma EDO linear de ordem. Vocês lembram como podemos resolvê-la?

Basicamente, temos uma solução geral para equações do tipo:
Ela vale:
Daí, como:
Substituindo na equação, vem:
Logo:
Em ambas as integrais, podemos fazer:
Logo:
Assim, temos:
Por fim:
Prontinho, deum um certo trabalho, mas conseguimos finalizar! Bora pro último item.
Passo 4
d) Pra finalizar a questão, precisamos apenas calcular a solução particular para a condição inicial , e determinar os valores de para os quais está definida.
Voltando na nossa solução geral, temos:
Para que esteja definida, ou seja exista, a função que determinamos precisa ser válida. Olhando para a nossa função , onde poderíamos ter problema?

É exatamente na raiz quadrada no denominador, pois além dela não poder ser negativa, como está no denominador também não pode ser nula. Assim:
Logo:
Ou seja, para que seja definido, precisamos ter .
Prontinho gente! Espero que vocês tenham entendido bem.
Até a próxima 😉
Resposta
a) Resolução no texto.
b)
c)
d)