Um sistema hexagonal é formado por hastes idênticas, de massa , e tem por vértices cinco partículas de massa e uma partícula de massa . Encontre a posição (,) do CM desse sistema, sabendo que cada lado do hexágono uniforme vale e que seu centro se encontra em (,). Justifique sua resposta.
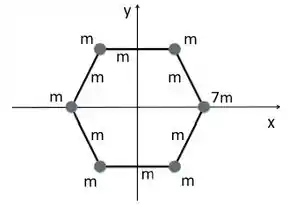
Passo 1
A posição do centro de massa, nada mais é do que uma média da posição de cada elemento de massa do sistema.
Poderíamos efetuar todos os cálculos com essas partículas e hastes, porém a saída é por meio da simetria...
Passo 2
Vamos trabalhar as simetrias do hexágono.
Começando pelas partículas.
Olhando para essas duas partículas aqui:
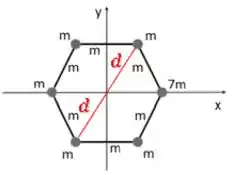
Como elas estão a uma mesma distância do centro, a média de suas posições é bem no meio, ou seja, no centro.
Mesma coisa pra essas aqui:
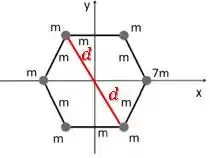
E pra essas, é o mesmo caso?
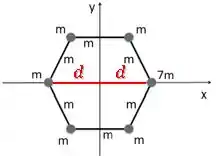
Não né!! Apesar de elas estarem a uma distância d do centro, elas possuem massas diferentes.
Beleza, então para as partículas, temos que as que fazem um “X” anulam uma a outra, por simetria. Essas que estão na horizontal precisam ser analisadas com mais calma.
Vamos dar uma olhada agora nas hastes.
Para cada haste do hexágono, há uma haste idêntica afastada de uma mesma distância do centro para o lado oposto. Então, cada haste anula a contribuição da haste oposta, já que todas tem a mesma massa.
Passo 3
Então se as partículas que fazem o “X” e as hastes não contribuem para o CM, pois cada uma anula a contribuição que está oposta, temos que a contribuição será dada somente pelas partículas na horizontal (que quebram a simetria, pois têm massas diferentes).
Como, e , temos:
Resposta
A posição do centro de massa é deslocada da origem para a direita, pois é a direita que se encontra a partícula com maior massa. Esse sistema apresenta uma simetria, onde alguns dos elementos de massa m e hastes apresentam um elemento idêntico, porém em posição oposta, de forma que não contribuem para o cálculo do CM.