Entre e , um corpo (1) de massa se move na direção horizontal positiva (), com velocidade . Ele então colide, em , com um corpo em repouso (2), de massa , e os dois corpos saem grudados.
a) Calcule a velocidade dos corpos 1 e 2 após a colisão.
Em , o corpo 2 explode enviando um fragmento de massa com uma velocidade na direção positiva do eixo .
b) Calcule a velocidade do resto do sistema após .
c) Calcule a velocidade do CM total (corpos 1 e 2, inteiros ou não) para , e .
Passo 1
Na primeira situação, temos uma colisão inelástica entre o corpo (1) com velocidade e o corpo (2) em repouso.
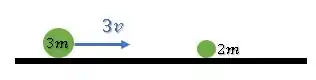
Como não há ação de forças externas (peso e normal se anulam), o momento linear do sistema se conserva:
Inicialmente, o momento linear será apenas o do corpo (1):
Já após a colisão, o momento linear será dos dois corpos que saem juntos:
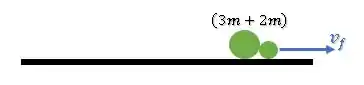
Aplicando na conservação de momento, temos:
Achamos a resposta da letra (a).
Passo 2
Agora, temos uma outra situação.
Vamos pensar num corpo com massa igual à soma das massas de (1) e (2) e velocidade que calculamos na letra (a).
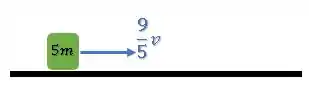
E esse corpo solta um fragmento de massa e velocidade :

Queremos achar a velocidade do blocão após liberar o fragmento.
Novamente, o momento linear do sistema se conserva, pois as forças que atuam nessa fragmentação são internas (o primeiro fragmento exerce força sobre o segundo, enquanto o segundo exerce a mesma força no sentido oposto sobre o primeiro).
Então:
Cortando a massa , ficamos com:
Essa é a velocidade do corpo que restou após lançar o fragmento, respondendo a letra (b).
Passo 3
Na letra (c), queremos a velocidade do centro de massa em cada intervalo de tempo.
A velocidade do centro de massa nada mais é do que uma média ponderada das velocidades de cada corpo do sistema, onde suas massas são os pesos dessa média.
Então, considerando um sistema de dois corpos, temos que a será:
Mas, calma lá!
Lembra que não há nenhuma força externa atuando nesse sistema ao longo de todos esses intervalos?
Então, se não há nenhuma força externa, não há nenhuma aceleração do centro de massa:
Ou seja, a velocidade do centro de massa será constante ao longo de todos esses momentos, independente das colisões e fragmentações:
E podemos calcular facilmente na situação onde existe um corpo só em movimento.
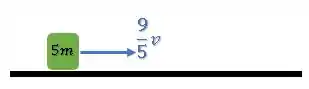
A velocidade do centro de massa será a própria velocidade do único corpo do sistema:
Masss, vamos calcular essas velocidades em cada um dos momentos para confirmar essa ideia e ainda por cima ver se não erramos nenhuma conta ao longo do desenvolvimento hahaha.
Passo 4
Intervalo de tempo antes da primeira colisão (), temos a seguinte situação:
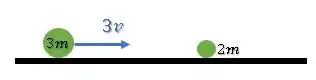
Ok!
Passo 5
No intervalo de tempo após a colisão e antes da fragmentação (), temos:
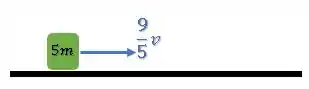
Aqui, a média da velocidade dos corpos do sistema será a própria velocidade do único corpo se movimentando.
Assim, temos que:
Ok também!
Passo 6
Já após a fragmentação (), temos:
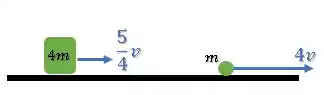
Então, a velocidade do centro de massa será:
Também bateu com o valor que esperávamos!
Confirmando assim, a nossa hipótese de que realmente a velocidade do centro de massa não se altera, uma vez que não há forças externas atuando no sistema.
Resposta
(a)
(b)
(c)
Em :
Em :
Em :