Um bloco de massa encontra-se a uma altura a partir do topo de uma mola relaxada de constante elástica . Use para a aceleração da gravidade. Após o bloco ser solto e tocar a mola, determine em termos de , e :
a) Qual a compressão da mola onde o bloco tem aceleração nula?
b) Determine a máxima compressão da mola.
Passo 1
A situação é a seguinte. Inicialmente o bloco é solto de uma altura acima da mola:
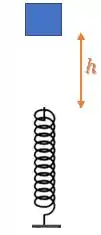
Queremos saber qual a compressão da mola onde o bloco tem aceleração nula.
Passo 2
Não podemos confundir aceleração nula com velocidade nula...
Pela Segunda Lei de Newton:
Vemos que a aceleração do bloco só será nula quando a força resultante sobre ele também for nula:
Passo 3
No momento em que o bloco toca a mola (não há compressão), há apenas a força peso atuando sobre ele:
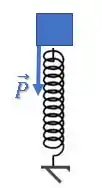
Na medida em que a mola vai se deformando, começa a atuar uma força elástica contrária, ou seja para cima:
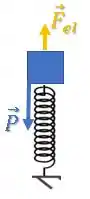
Entretanto, enquanto a força elástica é menor que a força peso , a resultante ainda é para baixo, ou seja, o bloco ainda tem uma aceleração para baixo.
Isso vai acontecer até que a deformação atinja um valor em que a força elástica tenha o mesmo módulo da força peso :
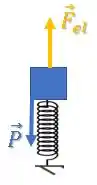
Nesse instante, a força resultante será nula:
Ou seja a aceleração será nula:
Por mais que o bloco ainda esteje em movimento de descida.
Passo 4
Então, basta igualar as duas expressões:
Passo 5
Já na letra (b), queremos achar a máxima deformação da mola.
Ou seja, queremos o instante em que a velocidade do bloco chegue a zero e ele não deforme mais a mola, voltando então a subir.
Se fizermos o raciocínio a partir das forças, será bastante trabalhoso já que a força elástica da mola é variável.
Então, uma boa alternativa é calcular isso através da energia.
Passo 6
Apenas as forças peso e elástica atuam sobre o bloco. Como elas são forças conservativas, a energia mecânica do sistema se conserva.
Então, vamos considerar o instante inicial com o bloco em repouso à uma altura da mola:
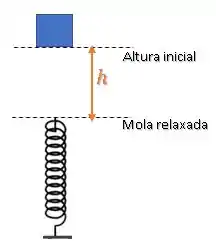
E o instante final, onde a deformação da mola é máxima:
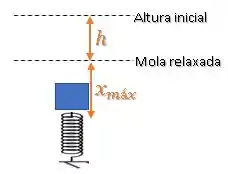
Passo 7
A energia mecânica inicial está apenas na forma de potencial gravitacional:
Onde a altura inical com base no referencial da menor altura é:
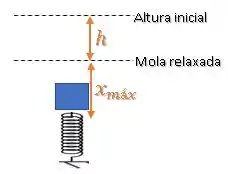
Então, a energia mecânica inicial é:
Já na situação final, o bloco novamente estará em repouso, portanto não vai ter energia cinética. Toda sua energia estará na forma de potencial elástica:
Aplicando na conservação de energia, temos:
Queremos isolar :
Temos uma equação de segundo grau:
Passo 8
Vamos aplicar na fórmula de Bháskara:
Substituindo as constantes , e , temos:
Poxa, mas temos dois valores possíveis então?
Nada disso!
Uma das raízes será negativa:
Isso acontece porque o termo resultante da raiz quadrada é maior que o termo , o que dá um negativo e por isso não será um resultado fisicamente plausível para essa situação.
Conseguimos descobrir isso olhando para o termo dentro da raiz.
Se dentro da raiz tivesse apenas o termo , teríamos:
Ou seja, nosso já seria nulo:
Porém, dentro da raiz temos mais um termo positivo somado e portanto o resultado dessa raiz é maior que:
Então, subtraindo esse termo, ficamos com um resultado negativo.
Pronto, eliminando esse resultado negativo de , ficamos apenas com o resultado positivo que é a nossa resposta:
Resposta
(a)
(b)