Uma partícula (1) de massa se move na direção positiva do eixo com velocidade no topo de uma mesa sem atrito de altura . Ao final da mesa encontra-se uma partícula (2) de massa . Ignore a dimensão das partículas.
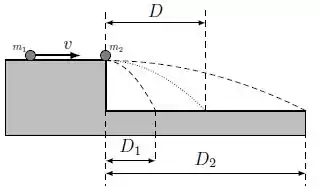
b) Supondo que a colisão entre as partículas foi perfeitamente inelástica, encontre a nova distância percorrida pelas partículas grudadas, em relação a base da mesa (na figura a distância é representada por , a trajetória é descrita pela linha pontilhada). O tempo de queda também é .
Passo 1
Nosso objetivo é achar o alcance das partículas no lançamento horizontal.
Para isso precisamos da velocidades das partículas no instante que elas saem da mesa.
Como a colisão, agora, é inelástica, as partículas sairão juntas. Ou seja, suas velocidades finais são as mesmas:
Então, basta nós descobrirmos essa velocidade final após a colisão e depois acharmos o alcance .
Passo 2
Como o sistema (duas partículas) não sofre a ação de forças externas, temos a conservação do momento linear:
Inicialmente, apenas a partícula (1) apresenta movimento, enquanto após a colisão, as duas partículas saem com a mesma velocidade:
Substituindo os valores das massas e da velocidade inicial :
Passo 3
Agora que temos a velocidade de saída da mesa, podemos olhar para o lançamento horizontal.
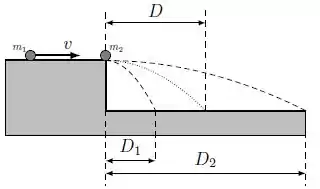
O problema já adiantou uma das etapas que é descobrir o tempo de queda e nos forneceu que esse tempo é:
Como na horizontal, as partículas realizam um movimento uniforme (não há aceleração horizontal), podemos usar a equação de :
Resposta
(b)