P1 de Física 1 da UFRJ - 2019.1

Um homem parado embaixo de uma marquise em uma rua nivelada horizontalmente vê as gotas de chuva caindo verticalmente com velocidade constante de módulo . Ao atravessar a rua correndo em linha reta ele percebe que as gotas de chuva, durante a travessia, caem com um ângulo em relação à horizontal. Se ele atravessou a rua com velocidade de módulo constante em relação à Terra, a resposta correta que permite obter o ângulo , é:

(a) )

(b)

(c)

(d)

(e)

Um bloco move-se sobre uma superfície horizontal com atrito. As forças que agem sobre o bloco estão indicadas no diagrama, a força faz um ângulo com a horizontal.

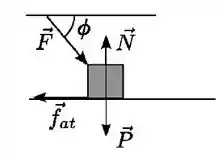
Se o bloco se move com velocidade constante, podemos afirmar que:

(a)

(b)

(c)

(d)

(e) Nada podemos afirmar porque não conhecemos o coeficiente de atrito

A figura abaixo mostra uma série de fotografias tiradas em intervalos de tempos iguais de uma barata voando em linha reta, no sentido da esquerda para a direita ( na direção positiva do eixo x).

Qual dos gráficos abaixo descreve de forma mais plausível o movimento da barata?

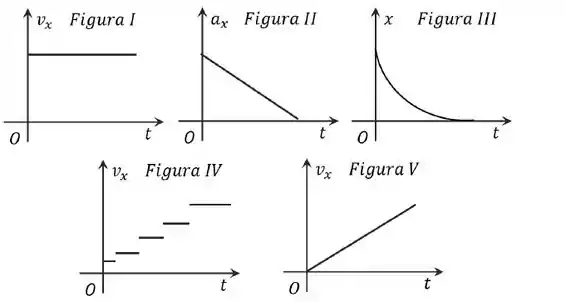
(a) Figura I

(b) Figura V

(c) Figura II

(d) Figura III

(e) Figura IV

(f) Nenhuma

Três macacos A, B e C, de mesma massa, estão pendurados em repouso, cada um em um cipó, com os cipós amarrados em um galho de árvore. Em um dado instante o macaco A sobe em seu cipó com velocidade constante, o macaco B sobe no seu com aceleração constante e o macaco C desce no seu com aceleração constante para baixo. Considerando que os cipós sejam fios ideais, que os movimentos aconteçam na vertical e sabendo que as acelerações mencionadas não são nulas, e denotando por , e as tensões nos cipós dos respectivos macacos A, B e C, podemos dizer que:

(a)

(b) e

(c)

(d)

(e) e

Um professor de física sai de sua casa e caminha a pé para o campus. Depois de . de caminhada, começa a chover. Ele então retorna para sua casa.

Sua distância em função do tempo é indicada pelo gráfico.

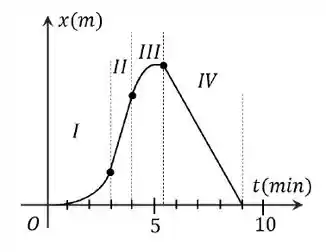
Observando o gráfico, podemos identificar 4 regiões diferentes, separadas temporalmente por linhas tracejadas, sobre estas regiões podemos afirmar que:

(a) Em nenhum momento a velocidade do professor é zero.

(b) Na região III o professor tem aceleração nula. Na região II a velocidade é constante e negativa

(c) Na região I o professor tem aceleração nula. Na região IV sua aceleração é máxima.

(d) Na região II o professor passa por um momento onde sua velocidade é nula. Na região IV a aceleração é constante e negativa.

(e) Em nenhum momento a velocidade do professor é constante.

(f) Na região III o professor passa por um momento onde sua velocidade é nula. Na região IV a velocidade é constante e negativa.

Dois blocos de massa e estão ligados por um fio ideal como ilustrado na figura abaixo.

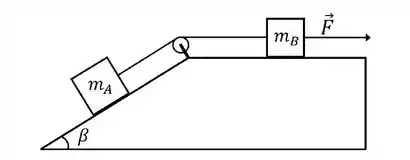
O bloco de massa desliza sobre a parte inclinada de um ângulo em relação à horizontal. Já o bloco de massa desliza sobre uma superfície plana. Sobre o bloco atua uma força de módulo paralela à horizontal. O coeficiente de atrito cinético entre os blocos e a superfície é igual .

Considerando que devido à ação da força o sistema passa a se mover para a direita:

a) Desenhe o diagrama de forças para cada um dos blocos.

b) Determine a aceleração do conjunto.

c) Determine a tensão no fio que une os blocos.

Suas respostas devem ser dadas em termos de ,, , , e .

Uma pequena esfera de massa m é presa na extremidade de um fio ideal de comprimento ` que tem sua outra extremidade presa a um ponto no teto, formando um pêndulo, como indicado na figura. A esfera é solta de uma posição horizontal, passando a se movimentar pela trajetória como a indicada.

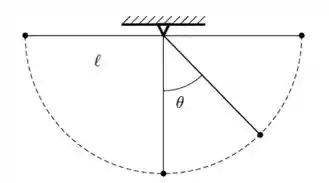
São feitas as seguintes observações sobre o movimento

do pêndulo:

I) Quando na posição mais baixa, a componente tangencial da aceleração possui seu valor máximo.

II) Quando a massa m passa pela posição mais baixa, temos que a tração feita pelo fio sobre a

massa é máxima.

III) A massa m descreve um movimento circular uniforme pois a resultante das forças é a centrípeta.

Quais das afirmações acima estão incorretas:

(a) I) e III)

(b) Apenas I)

(c) Apenas II)

(d) Apenas III)

(e) I) e II)

(f) II) e III)

Suponha que uma rã possa pular sempre com a mesma velocidade inicial em qualquer direção que ela pule (ela pode pular para frente ou diretamente de baixo para cima). Como a altura máxima () que ela pode atingir se relaciona com o alcance horizontal máximo ?

(a)

(b)

(c)

(d)

(e)

(f) Não há como saber sem conhecer o valor de .

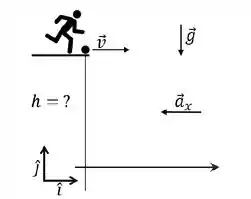
Um estudante chuta um rojão do alto de uma plataforma de altura acima do solo. O rojão é lançado com uma velocidade inicial horizontal de módulo . Entretanto, um forte vento que sopra paralelo ao solo faz com que o rojão tenha uma aceleração constante , sendo o módulo da componente horizontal da aceleração. Isso acaba por fazer com que o rojão caia no chão diretamente abaixo do estudante. Utilize o sistema de coordenadas indicado na figura e dê suas respostas em termos de , e .

a) Determine a altura da plataforma.

b) Determine o vetor velocidade do rojão imediatamente antes dele atingir o solo. Sua resposta deve ser dada em termos dos vetores unitários indicados na figura.

c) Qual é o alcance máximo, na horizontal, atingido pelo rojão em relação à plataforma?

Duas forças () agem sobre uma caixa de massa que desliza livremente sobre uma superfície plana. Na figura, temos uma vista de cima da situação, mas apenas uma força é mostrada além do vetor aceleração da caixa. Considerando que o módulo da força , a aceleração da caixa tem módulo igual a e o ângulo , a única afirmação incorreta é:

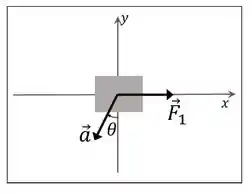
(a) O módulo da componente horizontal da força é maior do que o módulo da componente horizontal da força .

(b) O módulo da força resultante é igual a .

(c) A componente vertical da força resultante possui o mesmo módulo que a componente vertical da força

(d) O módulo da força é maior que o módulo da força resultante

(e) O módulo da componente horizontal da força é menor do que o módulo da componente horizontal da força .