Um homem parado embaixo de uma marquise em uma rua nivelada horizontalmente vê as gotas de chuva caindo verticalmente com velocidade constante de módulo . Ao atravessar a rua correndo em linha reta ele percebe que as gotas de chuva, durante a travessia, caem com um ângulo em relação à horizontal. Se ele atravessou a rua com velocidade de módulo constante em relação à Terra, a resposta correta que permite obter o ângulo , é:
(a) )
(b)
(c)
(d)
(e)
Passo 1
Enquanto o homem tá parado ele vê a chuva caindo assim:
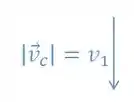
Aí o homem atravessa a rua com velocidade assim:
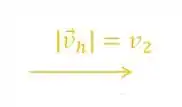
Então para o homem, as gotas de água viajam assim:
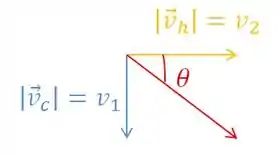
Pronto!
Calculando a tangente do ângulo:
Show?
Resposta
Alternativa A.
Exercícios de Livros Relacionados
Um avião pequeno atinge uma velocidade do ar de 500k m / h . O piloto pretende chegar a um ponto 800k m ao norte, mas descobre que deve direcionar o avião 20,0 ° a leste do norte para atingir o destin
A ‘esteira rolante horizontal’ do terminal de um aeroporto se move a 1,0m/s e tem 35,0m de comprimento. Se uma mulher pisa em uma das extremidades e caminha a 1,5m/s em relação à plataforma móvel, qua
Dois píeres estão localizados em um rio: o píer B está situado a 1500 m de A corrente abaixo (Figura 3.35). Dois amigos devem fazer um percurso do píer A ao píer B e depois voltar. Umdeles vai de barc
Voos longos em latitudes médias no Hemisfério Norte encontram a chamada corrente de jato, um fluxo de ar para leste que pode afetar a velocidade do avião em relação à superfície da Terra. Se o piloto
Um rio de 1km de largura tem uma correnteza de velocidade 1,5 km/h. Um homem atravessa o rio de barco, remando a uma velocidade de 2,5 km/h em relação à água. a) Qual é o tempo mínimo que leva para at