Três macacos A, B e C, de mesma massa, estão pendurados em repouso, cada um em um cipó, com os cipós amarrados em um galho de árvore. Em um dado instante o macaco A sobe em seu cipó com velocidade constante, o macaco B sobe no seu com aceleração constante e o macaco C desce no seu com aceleração constante para baixo. Considerando que os cipós sejam fios ideais, que os movimentos aconteçam na vertical e sabendo que as acelerações mencionadas não são nulas, e denotando por , e as tensões nos cipós dos respectivos macacos A, B e C, podemos dizer que:

(a)

(b) e

(c)

(d)

(e) e

Vamos entender o que está acontecendo.

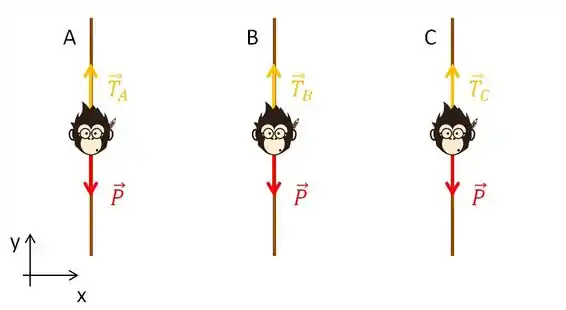
Temos os 3 macacos, de mesma massa. Um em cada cipó. Já representei as forças ali na figura.

Além disso, o enunciado fala pra gente que:

A sobe em seu cipó com velocidade constante. Então a segunda lei de Newton para A, fica:

Se a velocidade é constante, então .

Logo

Outra coisa que o enunciado fala pra gente é:

B sobe no seu com aceleração constante. Então a segunda lei de Newton para B, fica:

Aqui a gente já vê que:

A outra coisa que ele fala no enunciado é:

C desce no seu com aceleração constante para baixo. Então a segunda lei de Newton para C, fica:

Então, temos que:

Olhando para as alternativas, vemos que a letra b é a que se encaixa!