A figura abaixo mostra uma série de fotografias tiradas em intervalos de tempos iguais de uma barata voando em linha reta, no sentido da esquerda para a direita ( na direção positiva do eixo x).
![]()
Qual dos gráficos abaixo descreve de forma mais plausível o movimento da barata?
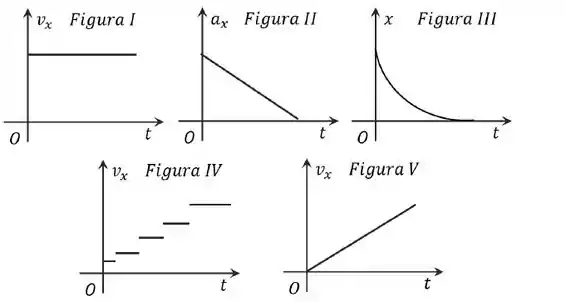
(a) Figura I
(b) Figura V
(c) Figura II
(d) Figura III
(e) Figura IV
(f) Nenhuma
Passo 1
Fala aí!! Vamos olhar pra essa figura com calma:
![]()
As marcas estão mostrando a posição da barata no tempo.
Agora olhem para o espaçamento das marcas. Perceberam? O espaçamento aumenta conforme o tempo aumenta. Ou seja, não é uma relação linear.
Se fizermos o gráfico da posição pelo tempo da barata teremos:
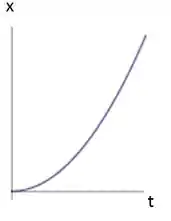
Se a posição varia de forma quadrática com o tempo , ou seja, obedece essa equação:
Temos que a velocidade varia de forma linear com o tempo.
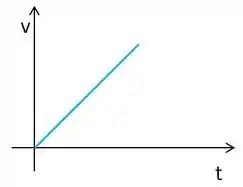
E se a velocidade é linear com o tempo, temos que a aceleração é constante.
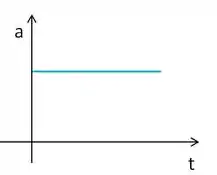
Passo 2
Comparando esses gráficos com as nossas opções, temos que a resposta é a FIGURA V.
Resposta
Alternativa B.