Um professor de física sai de sua casa e caminha a pé para o campus. Depois de . de caminhada, começa a chover. Ele então retorna para sua casa.
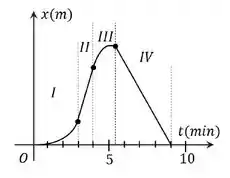
Sua distância em função do tempo é indicada pelo gráfico.
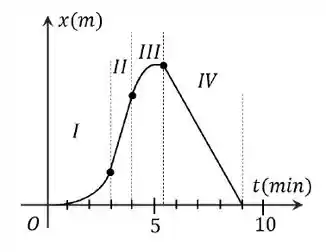
Observando o gráfico, podemos identificar 4 regiões diferentes, separadas temporalmente por linhas tracejadas, sobre estas regiões podemos afirmar que:
(a) Em nenhum momento a velocidade do professor é zero.
(b) Na região III o professor tem aceleração nula. Na região II a velocidade é constante e negativa
(c) Na região I o professor tem aceleração nula. Na região IV sua aceleração é máxima.
(d) Na região II o professor passa por um momento onde sua velocidade é nula. Na região IV a aceleração é constante e negativa.
(e) Em nenhum momento a velocidade do professor é constante.
(f) Na região III o professor passa por um momento onde sua velocidade é nula. Na região IV a velocidade é constante e negativa.
Passo 1
Vamos fazer uma revisão de análise de gráficos aqui rapidinho, e depois a gente vê as alternativas.
Em um gráfico a velocidade é dada pelo coeficiente angular da curva, ou seja a tangente, pois
Isso quer dizer que se o gráfico for uma reta então a velocidade é constante, porque a inclinação se mantém a mesma, a velocidade vai ser positiva, se a reta for crescente; e negativa se a reta for decrescente.
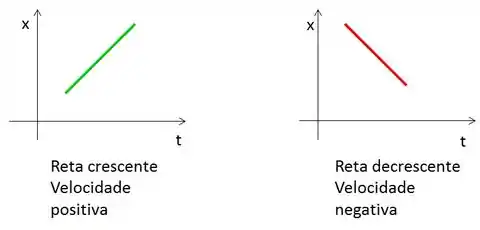
Se o gráfico for uma curva, então a velocidade varia, pois a inclinação da reta tangente varia, logo, é um MUV. E temos aceleração. Mas essa relação da velocidade ainda vale. Olha só:
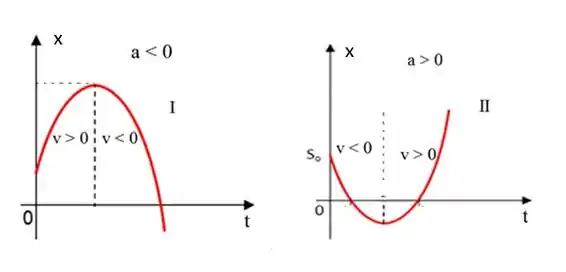
Pronto... vamos ver as opções agora.
Passo 2
(a) Em nenhum momento a velocidade do professor é zero.
Falsa né! Por 2 motivos:
1) Interpretação: quando começa a chover o professor vai retornar pra casa dele. Então se ele tava indo, ele tem que parar e virar pra voltar. Então a velocidade foi zero nesse instante.
Mas como a gente vê isso no gráfico??
Vamos lá:
2) Nós vimos que
Pra velocidade ser zero, temos:
Ou seja, a tangente da curva . Isso só acontece quando temos pedacinhos do gráfico horizontais. Que é o que ocorre no intervalo III.
Passo 3
(b) Na região III o professor tem aceleração nula. Na região II a velocidade é constante e negativa
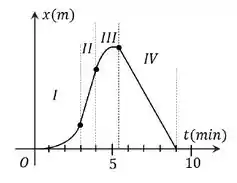
Nós vimos que na região III a VELOCIDADE é nula. A aceleração é negativa na região 3, pois a concavidade está pra baixo, certo?
E a na região II, temos um segmento de reta, então a velocidade é constante . Mas a reta é crescente, então a velocidade é POSITIVA.
Logo, essa alternativa tá errada.
Passo 4
(c) Na região I o professor tem aceleração nula. Na região IV sua aceleração é máxima.
Na região I temos uma curva, então a velocidade varia, logo a aceleração é não nula e , nesse caso, positiva.
Na região IV, temos um linha reta, logo a velocidade é constante, e a aceleração é nula!!
Essa também está errada!
Passo 5
(d) Na região II o professor passa por um momento onde sua velocidade é nula. Na região IV a aceleração é constante e negativa.
A velocidade é nula na região III (pedacinho da reta horizontal).
Na região IV, a VELOCIDADE que é constante e negativa. Aqui a aceleração é zero.
Erradíssima
Passo 6
(e) Em nenhum momento a velocidade do professor é constante.
Falsa!! Já vimos que nas regiões II e IV a velocidade é constante (por causa dos segmentos de reta).
Passo 7
(f) Na região III o professor passa por um momento onde sua velocidade é nula. Na região IV a velocidade é constante e negativa.
Certa!! Na região III temos
E na região IV temos um segmento de reta decrescente.
Resposta
Alternativa F.